خروجی سیستم دینامیکی آونگ با متلب
سیستم دینامیکی آونگ با متلب
برای حل مسئله دینامیکی آونگ، 2 حالت را برای حل در نظر گرفتیم. در حالت اول یک شتاب ثابت به سیستم اعمال کردیم و خروجی سیستم دینامیکی را ترسیم کردیم. برای داشتن یک حالت کلی تر و حرفهای تر، یک شتاب هارمونیک به سیستم اعمال کردیم و خروجی ها را بررسی کردیم.
فایلهای این شبیه سازی در انتهای همین صفحه جهت دانلود رایگان قرار گرفته است.
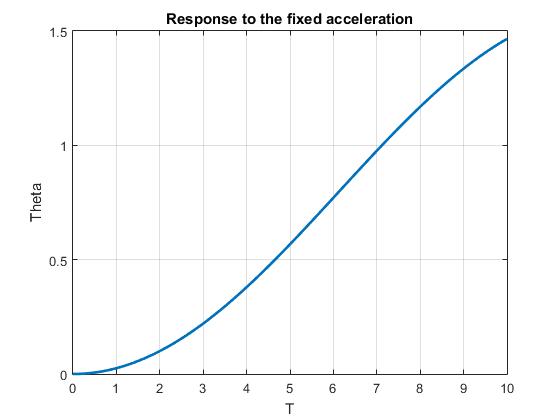
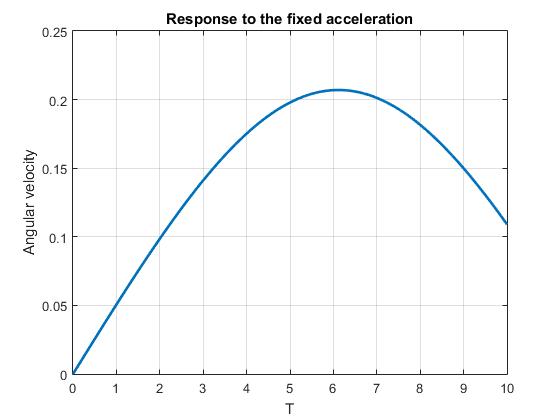
در پوشه P1 حالت اول را اعمال کردیم. کد نویسی مسئله به این صورت است که معادلات دینامیکی را در تابع pendulum1 نوشته و این معادلات را در کد p1 ، با کمک تابع ode45 برای زاویه و سرعت زاویهای اولیه 0 و 0 حل کردیم. لازم به ذکر است که شتاب را 5 متر بر مجذور ثانیه در نظر گرفتیم. بقیه پارامترهای سیستم همانند حل دستی ضمیمه شده به طور دلخواه انتخاب شدهاند. دو نمودار برای خروجی چاپ می شود.
انجام پروژه متلب با متلبی
پروژه متلب ازقرار زیر است:
%%%% Fixed Acceleration
t=0:0.01:10;
l=0.25;
k=7;
a=10;
x=-15/.5^2*cos(0.5*t)+15/0.5^2;
A=[a;k;l];
[t,th]=ode45(‘pendulum1′,t,[0 0],[],A);
figure
plot(t,th(1:end,1),’LineWidth’,2)
grid on
xlabel(‘T’);
ylabel(‘Theta’);
title(‘Response to the fixed acceleration’)
saveas(gcf,’1.pdf’);
نمودار اول در واقع زاویه
انجام پروژه متلب با متلبی
و در ادامه داریم:
figure
plot(t,th(1:end,2),’LineWidth’,2)
grid on
xlabel(‘T’);
ylabel(‘Angular velocity’);
title(‘Response to the fixed acceleration’)
saveas(gcf,’2.pdf’);
و نمودار دوم سرعت زاویه ای
آونگ می باشد. لازم به ذکر است که این خروجی ها بعد از هر اجرا به شکل خودکار در دو فایل پی دی اف 1 و 2 با کیفیت مطلوبی ذخیره می شوند.
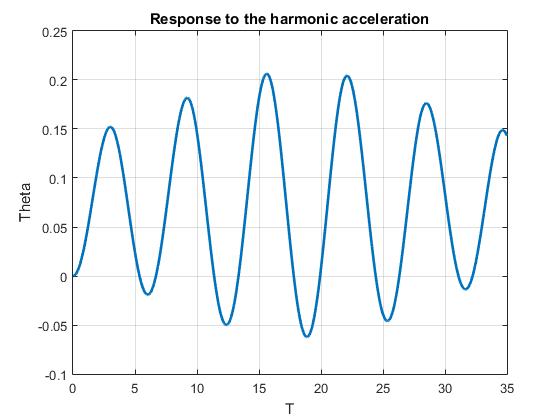
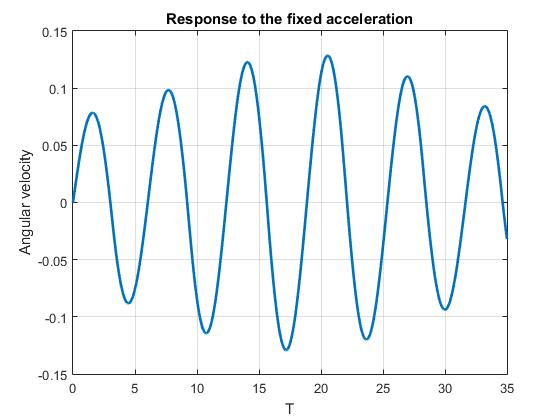
در ادامه کار یک شتاب هارمونیک به سیستم اعمال کردیم و روند بالا را دنبال شد. حالت شتاب ثابت و هارمونیک را در یک کد نوشته و در پوشه p2 قرار گرفته اند.
انجام پروژه متلب با متلبی
در ادامه برنامه متلب فوق داریم:
%%%% Harmonic Acceleration
t1=0:0.01:35;
l1=0.25*ones([1,length(t1)]);
k1=10*ones([1,length(t1)]);
a1=15*cos(0.5*t1);
x1=-15/.5^2*cos(0.5*t)+15/0.5^2;
A1=[k;l];
معادلات دینامیکی آونگ در فانکشن pendulum قرار دارد و با دستور ode این معادله را محاسبه کرده ایم:
[t1,th1]=ode45(‘pendulum’,t1,[0 0],[],A);
figure
plot(t1,th1(1:end,1),’LineWidth’,2)
grid on
xlabel(‘T’);
ylabel(‘Theta’);
title(‘Response to the harmonic acceleration’)
saveas(gcf,’3.pdf’);
زاویه آونگ در شتاب هارمونیک
سپس
figure
plot(t1,th1(1:end,2),’LineWidth’,2)
grid on
xlabel(‘T’);
ylabel(‘Angular velocity’);
title(‘Response to the fixed acceleration’)
saveas(gcf,’4.pdf’);
و سرعت زاویه ای:
تابع pendulum که شامل معادلات دینامیکی آونگ هست نیز به صورت زیر پیاده شده اند:
function out=pendulum(t,x,flag,A)
k=A(1,1);
l=A(2,1);
g=9.81;
A0=1.1;
out=[x(2);1/k^2*(sign(cos(0.5*t))*A0*cos(0.5*t)*l*cos(x(1))-g*l*sin(x(1)))];
و برای pendulum1 در سیستم دینامیکی آونگ با متلب بصورت زیر داریم:
function out=pendulum1(t,x,flag,A)
k=A(2,1);
l=A(3,1);
a=A(1,1);
g=9.81;
out=[x(2);1/k^2*(a*l*cos(x(1))-g*l*sin(x(1)))];
این پروژه متلب با هدف آشنایی با معادلات سیستم آونگ و گرفتن خروجی در شرایط شتاب ثابت و هارمونیک برای مخاطبین خوب سایت متلبی منتشر شده است.
سفارش انجام پروژه مشابه
درصورتیکه این پروژه و آموزش متلب دقیقا مطابق خواسته شما نمی باشد، با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.


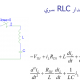

ممنون بابت قرار دادن سورس کد متلب
درود بر شما, ممنون از فیدبک مثبتتون