
انتخاب پیش فرض یک ورژن متلب از بین چند ورژن متلب
/
0 نظرات
انتخاب پیش فرض یک ورژن متلب از بین چند ورژن متلب
اگر روی وین…
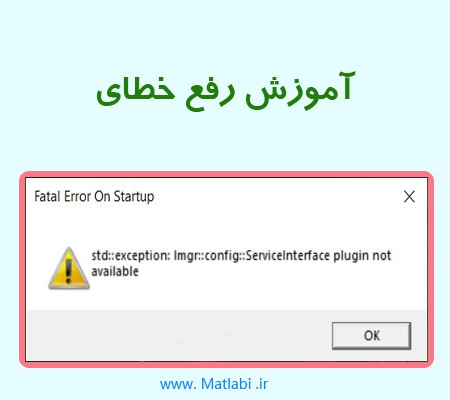
خطای Fatal Error On Startup هنگام اجرای متلب
خطای Fatal Error On Startup هنگام اجرای متلب
این خطا بعد از نصب متلب …

رفع مشکل اجرا نشدن setup.exe در زمان نصب متلب
رفع مشکل اجرا نشدن setup.exe در زمان نصب متلب
نرم افزار متلب را …

آموزش رفع خطای License Error –4,0 موقع اجرا کردن Polyspace متلب
آموزش رفع خطای License Error –4,0 موقع باز کردن Polyspace متلب
…
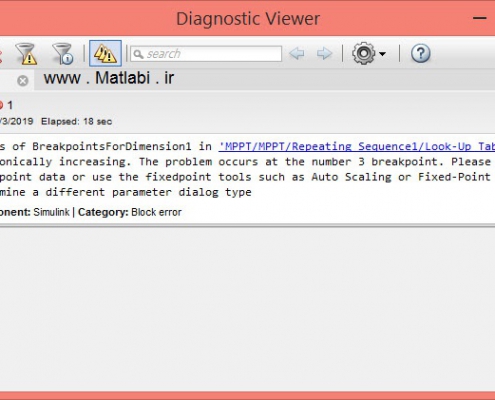
رفع خطای must be monotonically increasing در سیمولینک متلب
رفع خطای must be monotonically increasing در سیمولینک متلب
در این پست …

آموزش نصب متلب 2019 , رفع مشکل نصب متلب 2019a
آموزش نصب متلب 2019 | رفع مشکل نصب متلب 2019a
در این پست قصد دار…
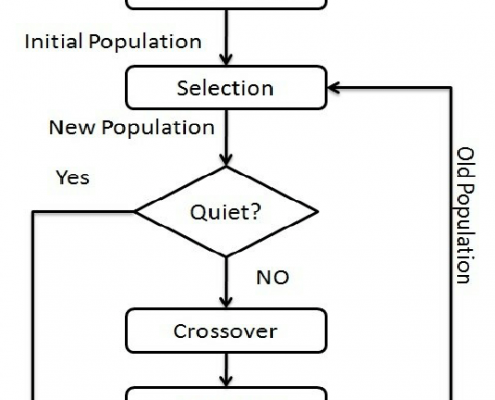
آموزش و دانلود الگوریتم ژنتیک
آموزش و دانلود الگوریتم ژنتیک
برای آموختن الگوریتم ژنتیک منابع …
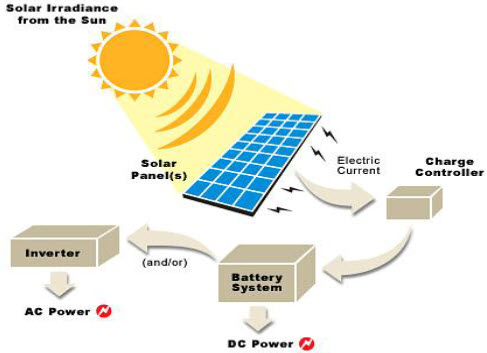
سلول های خورشیدی و بررسی سیستم های فتوولتائیک (PV) بهمراه مدلسازی در متلب
سلول های خورشیدی و بررسی سیستم های فتوولتائیک(PV)
در این پست …
 https://www.matlabi.ir/wp-content/uploads/2019/05/matpower.jpg
450
450
matlabi
https://www.matlabi.ir/wp-content/uploads/2020/05/logo-matlabi.png
matlabi2019-05-17 19:20:342020-07-24 15:08:31تولباکس مت پاور | MATPOWER toolbox
https://www.matlabi.ir/wp-content/uploads/2019/05/matpower.jpg
450
450
matlabi
https://www.matlabi.ir/wp-content/uploads/2020/05/logo-matlabi.png
matlabi2019-05-17 19:20:342020-07-24 15:08:31تولباکس مت پاور | MATPOWER toolbox