نوشتهها
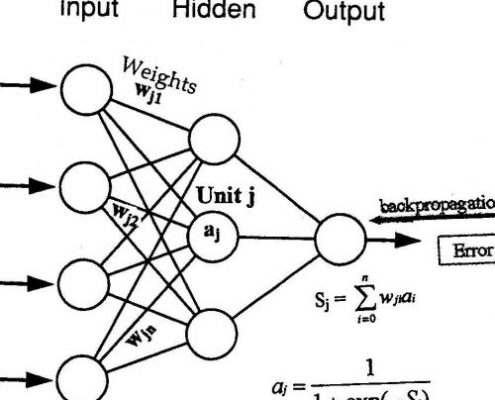
پیش بینی سری زمانی به کمک شبکه عصبی در متلب
/
0 نظرات
پیش بینی سری زمانی به کمک شبکه عصبی در متلب
خلاصه مبحث آموزشی …
شناسایی توابع انتقال ماشین DCبا استفاده از پاسخ پله به کمک الگوریتم ژنتیک
پروژه درس شناسایی سیستم
عنوان پروژه :
شناسایی توابع انتقال ماشین …
پروژه کامپیوتری درس فرایند تصادفی با متلب
پروژه کامپیوتری درس فرایند تصادفی با متلب
با یک آموزش متلب دیگ…
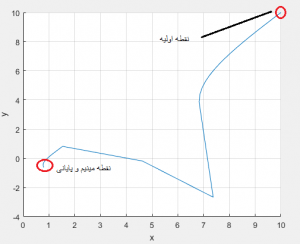
حل تابع با سری تیلور و روش نیوتن در متلب
حل تابع با سری تیلور و روش نیوتن در متلب
دستور متلب
syms x…

دانلود نرم افزار متلب Mathworks Matlab 2017a
Mathworks Matlab یک نرم افزار قوی جهت شبیه سازی و کدنویسی برای …
 https://www.matlabi.ir/wp-content/uploads/2015/10/Matlab_Logo1.jpg
726
808
matlabi
https://www.matlabi.ir/wp-content/uploads/2020/05/logo-matlabi.png
matlabi2014-11-25 11:57:112021-04-27 01:50:12متلب چیست؟
https://www.matlabi.ir/wp-content/uploads/2015/10/Matlab_Logo1.jpg
726
808
matlabi
https://www.matlabi.ir/wp-content/uploads/2020/05/logo-matlabi.png
matlabi2014-11-25 11:57:112021-04-27 01:50:12متلب چیست؟