شناسایی توابع انتقال ماشین DCبا استفاده از پاسخ پله به کمک الگوریتم ژنتیک
پروژه درس شناسایی سیستم
عنوان پروژه :
شناسایی توابع انتقال ماشین DC با استفاده از پاسخ پله به کمک الگوریتم ژنتیک
انتخاب مدل مناسب برای سیستم
انتخاب مدل مناسب در فرآیند طراحی و شناسایی موضوع بسیار مهم می باشد.
انتخاب یک مدل اشتباه باعث انجام محاسبات اضافی و از دست دادن زمان خواهد شد.
مدل های مختلفی که عموماَ وجود دارد و از آنها جهت انجام تحقیقات استفاده می شود به صورت زیر می باشد که در زیر هر یک از مدل ها را توضیح می دهیم:
الف: مدل جعبه سیاه
ب: مدل جعبه خاکستری
ج: مدل جعبه سفید
الف) مدل جعبه سیاه
در این مدل اجزای داخلی توصیف نمی شوند و مدل مسئله را به صورت عددی و بدون زمینه فیزیکی حل می کند.
این مدل معمولاً به شکل مجموعه ای از پارامتر های انتقال و یا قوانین تجربی که خروجی مدل را به ورودی مرتبط می کند بیان می شود.
به عنوان مثال هنگامی که ترانزیستور به عنوان یک منبع جریان وابسته به جریان مدل می شود این مدل یک مدل جعبه سیاه است.
در این مدل اجزای داخلی ترانزیستور مخفی می باشند.
در چنین مدلی نسبت جریان خروجی به بیس جریان ترانزیستور برابر بهره جریان می باشد.
ب) مدل جعبه خاکستری
در مدل برخی یا تمامی مکانیزم هایی که رفتار اجزای داخلی را توصیف می کنند بیان می شود البته نه به طور کامل.
در مدل جعبه خاکستری، المان های داخلی مدل با قوانین تقریبی بیان می شوند.
مدل جعبه خاکستری ترانزیستور نسبت به حالت قبل پیچیده تر خواهد بود و برخی از عملکرد ها یا عملیات داخلی ترانزیستور را بیان می کند.
به عنوان مثال مدل Ebers Moll ترانزیستور یک مدل جعبه خاکستری می باشد. در این مدل ها نیز برخی از تقریب ها به کار گرفته شده است.
ج) مدل جعبه سفید
در مدل جعبه سفید بیشترین مقدار جزئیات را برای شبیه سازی باید فراهم داشته باشیم و هیچ تقریبی در آن به کار نرفته است.
مدلی با چنین جزئیاتی فقط هنگامی استفاده می شود که به نتایج شبیه سازی کاملاً دقیقی نیاز باشد.
زیرا این مدل محاسبات زیادی در پی خواهد داشت.
مدل کامل جعبه سفیدی از ترانزیستور وجود ندارد. مدل Ebers Moll را نمی توان به عنوان یک مدل جعبه سفید در نظر گرفت.
برای مثال مدل جعبه سفید بایستی حرکت الکترون ها و نگه داشتن آنها توسط حفره ها در P را نشان دهد.
انتخاب بین این سه مدل بستگی جزئیات مورد نظر دارد.
شناسایی توابع انتقال ماشین DC
با استفاده از پاسخ پله به کمک الگوریتم ژنتیک
شاید به مطالب زیر نیز علاقه مند باشید:
- تشخیص فونم ها(لب خوانی) با SVM در متلب
- طراحی و پیاده سازی OCR دست نویس فارسی با استفاده از عناصر ابتدایی تشکیل دهنده حروف
- قسمت دوم بانک مقالات شبیه سازی شده برق کنترل
- مدل فرایند گاورنر 4درجه آزادی جهت کنترل سرعت توربین
- مقالات شبیه سازی شده در متلب- پردازش سیگنال و هوش مصنوعی
چکیده :
در ابتدا قصد داریم کار انجام شده در مقاله را توضیح داده و سپس به بررسی شبیه سازی انجام شده توسط خودمان بپردازیم.
مقاله مورد نظر مربوط به تخمین پارامتر های شبیه سازی موتور DC با استفاده از الگوریتم ژنتیک در مقایسه با روش تخمین حداقل مربعات می باشد.
این مقاله بر اساس سیستم های تک ورودی تک خروجی استوارمی باشد.
کاری را که ما انجام داده ایم سیستم را به صورت یک سیستم چند متغییره با دو ورودی و دو خروجی در نظر گرفته ایم که توضیحات تکمیلی در ادامه آمده است.
کار انجام شده در مقاله :
دراین مقاله هدف تخمین پارامتر های دینامیکی موتور DC با استفاده از الگوریتم ژنتیک می باشد.
جهت مقایسه با روش تخمینی بر اساس الگوریتم ژنتیک ، استفاده از روش LSE مناسب به نظر می رسد.
با وجود این که تخمین با استفاده از روش LSE بر اساس تابع خطای خطی صورت گرفته است ، روش GA به آسانی می تواند به آسانی پارامتر های ناشناخته را شناسایی کرده البته با استفاده از مینیمم کردن جمع مربعات خطا.
همچنین مدل ما می تواند غیر خطی نیز باشد و در این شناسایی سیستم بون نویز و تحریک گذرا در نظر گرفته شده است.
در نهایت در این مقاله مقایسه ای بین بهینه سازی های انجام شده توسط GA و LSE انجام گرفته است و نشان داده شده است که GA لحاظ وضوح و قدرت در تخمین پارامتر ها به مراتب از سایر روش ها در در مرتبه بالاتری قرار دارد.
هنگامیکه مطالعات حالت های دینامیکی یک سیستم و یا موضوع طراحی انواع کنترل کننده ها برای یک سیتم مطرح باشد؛ توابع انتقال بهترین ابزار برای معرفی سیستم است.
از این جهت مبحث شناسایی توابع انتقال سیستم ها از جمله موضوعاتی است که امروزه مورد توجه فراوان واقع شده است.
ماشین های dc یکی از انواع ماشین های الکتریکی بوده که به لحاظ دارا بودن محدوده عملکرد وسیعی در سرعت و ولتاژ و برخورداری از مشخصات کنترلی مطلوب، کاربرد آن رو به گسترش است.
تاکنون روش های مختلفی جهت تعیین توابع انتقال ماشین dc به منظور مطالعات دینامیکی و کنترلی آن پیشنهاد شده است.
در این مقاله با استفاده از معادلات حالت ماشین dc یک تابع انتقال برای ماشین فرض شده و پارامترهای این تابع با تعیین پاسخ پله ماشین و توسعه روشی بر مبنای الگوریتم ژنتیک بدست آمده است.
این مطالعه مدل خطی نسبتا دقیقی از ماشین dc ارائه می دهد.
مقدمه
به منظور انجام یک تحلیل نظری از شناسایی سیستم، لازم است که فرض هایی را در نظر بگیریم.
در بعضی موارد برای توصیف، روابط ریاضی بکار می روند.
در عمل هنگامی که داده های واقعی استفاده می شود سیستم ناشناخته است و حتی می توان آن را ایده آل فرض کرد.
در این مقاله رفتار دینامیکی موتور DC با روش تخمین پارامتر های پیشنهاد شده، مطرح شده است .[1]
شناسایی سیستم عموماً شامل دو مدل می شود،1-مدل های غیر پارامتری و2-مدل های پارامتری.
مدل های غیر پارامتری، مربوط به مدل هایی می شود که با منحنی، تابع و یا جدول توصیف شده اند.
اما در بسیاری از موارد مناسب است که با مدل های پارامتری سروکار داشته باشیم.. [1]
بطور کلی شرایط آزمایشی توصیفی هستند از اینکه چگونه آزمایش شناسایی انجام می شود.
این شامل انتخاب و تولید سیگنال ورودی،بازه نمونه برداری، پیش فیلترینگ اطلاعات ابتدایی و تخمین پارامترها می شود.
قبل از گردش به سمت تخمین پارامتر های موتور دینامیکی موتور DC این نکته باید یادآوری شود که مدل سیستم بایستی ثابت باشد.
در این مقاله ، کاربردهای بهینه سازی الگوریتم ژنتیک را در روش شناسایی پارامتری معرفی می کنیم.
پارامتر های ناشناخته هنگامی که مینیمم سازی تابع خطا به پایان برسد، بدست می آیند.
برای استفاده از الگوریتم ژنتیک در مسئله تخمین پارامتر، ابتدا بایستی فرمول تابع برازندگی را مطابق با مجموع مربعات خطا بدست آورد.
الگوریتم با یک تخمین اولیه از پارامترها شروع می شود.
سپس الگوریتم رشته ای از تخمین پارامتر های جدید را بوجود می آورد.در هر مرحله، الگوریتم از تخمین های کنونی برای تولید تخمین های بعدی استفاده می کند.
2-در باره این روش
روش پیشنهادی بر اساس مراحل زیر می باشد:
الف-فرض می شود G یک سیستم LTI می باشد که مدل مشخص آن تعریف نشده می باشد(ما تنها تعداد قطبها و نوع آن را توانیم حدس بزنیم) بنابراین H(s) (تابع تبدیل تخمینی سیستم) می تواند در حوزه تبدیل لاپلاس به شکل زیر بیان شود:
ب-فرض می شود که سیستم شامل N1 قطب حقیقی و قطب مختلط باشد.
بنابراین بسط کسری شکسته H(s) به شکل زیر بدست می آید:
که در آن پارامتر های ناشناخته هستند.
ج-فرض می شود که سیستم با یک تابع پله به عنوان ورودی سیستم تحریک شود:
شکل شماره 1 .مدل فرض شده
در نتیجه پاسخ پله سیستم می تواند به شکل زیر محاسبه شود:
اگر عکس تبدیل لاپلاس H(s) موجود باشد y(t) را می توان به سادگی محاسبه کرد.
د-بعد از محاسبه y(t) پارامترهای ناشناخته(معادلات 2 و 3و4) مدل زیر قابل اجرا می باشد.
شکل2- مدل تخمینی
0<i<N ،G یک سیستم غیر قابل دسترس می باشد (تنها نقاط داده خروجی در دسترس می باشند) و y(t) تابع تخمین پارامتر های ناشناخته می باشد.
حال برای هر زمان نمونه برداری مطرح می شود.
یک عدد حقیقی و تابعی از پارامترهای ناشناخته در زمان نمونه برداری می باشد.
h(t) ازهر اطلاعاتی در رابطه با محل قطب ها یا حدس حالت دینامیکی مدل بدست می آیدو ما h(t) ویا H(s) مطابق با مدل مشخص را نداریم، بنابراین اگر مدل مشخصی در دسترس بود مسئله بسیار ساده می بود)
ه-در این مرحله هدف مینیمم کردن مربع تابع خطا و بدست آوردن پارامترهای ناشناخته می باشد.
و-به عنوان تابع برازندگی مطرح شده و با استفاده از روش بهینه سازی الگوریتم ژنتیک مینیمم می شود.
شاید به مطالب زیر نیز علاقه مند باشید:
- دانلود نرم افزار متلب Mathworks Matlab 2017a
- آموزش انجام پروژه درس کنترل مدرن با متلب
- قسمت دوم بانک مقالات شبیه سازی شده برق کنترل
- پروژه کامپیوتری درس فرایند تصادفی با متلب
- سفارش شبیه سازی مقالات درس کنترل مدرن با متلب
- انجام پروژه متلب با سایت متلبی
طرح مسئله
هدف ما شبیه سازی هر موتور DC با تخمین حالت دینامیک آن می باشد.
معادلات حالت ماشین dc بصورت زیر می باشند:
که در آن جریان آرمیچر و سرعت زاویه ای روتور می باشد.
پارامتر های موتور DC می باشد که در جدول 1 شرح آن موجود می باشد.
بر اساس مرجع شماره [4] طرز عمل و استفاده ازموتور DC می تواند به صورتزیر مدل شود :
شکل 3 مدل دینامیکی مرتبه دوم
که در آن نسبت میرایی و فرکانس طبیعی میرا نشده و K بهره سیستم می باشد. هدف شناسایی این سه پارامتر با استفاده از حداقل مربعات خطا به صوت مدل زیر:
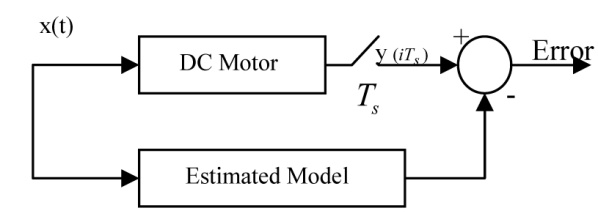
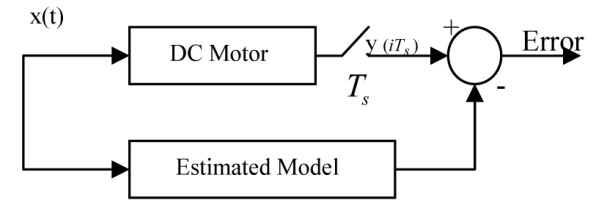
شکل 4 بلوک دیاگرام تخمین پارامتر
پارامتر های تست شده موتور را به صورت زیر در نظر بگیرید:
جدول 1
پارامتر های تست شده موتور
بر اساس معادلات (2) و (3) و (4) و شکل 3 ما تنها یک بخش مرتبه دوم داریم، از این رو معادله (9) به صورت زیر می باشد:
که H(s) مدلی است که قرار است پارامتر های آن تخمین زده شود.
باتوجه به معادله (9) معادلات 10 و 11 را به صورت زیر داریم :
در زیر مدل ایجار شده در محیط سیمولینک را می توانید مشاهده نمایید :
در نهایت تابع برازندگی به صورت معادله 12 در نظر گرفته می شود. پاسخ پله تست شده موتور DC به صورت زیر می باشد :
شکل5. پاسخ پله موتور تست شده
اکنون سعی می کنیم با استفاده از روش الگوریتم ژنتیک پارامتر های مدل ناشناخته خود را شناسایی نماییم.
که در انتهای این مقاله از تخمین LSE جهت مقایسه با این روش استفاده شده است .
توجه شود که محاسبات انجام شده بر اساس تحریک گذرا می باشد.
برای سادگی کار پارامتر های و K را پارامتر های مجهول و را به عنوان پارامتر معلوم در نظر می گیریم ().
تخمین پارامتر بر اساس الگوریتم ژنتیک
الگوریتم ژنتیک یک الگوریتم بهینه سازی تصادفی می باشد که در ابتدا با یک مکانیزم انتخاب طبیعی شروع شده و با ژنتیک تکامل می یابد.
در پایین الگوریتم تخمین پارامتر بر اساس GA توسعه داده شده که پارامتر های ناشناخته را با مینیمم کردن تابع برازندگی تخمین بزند.
اپراتور GA
مراحل عملیات انجام شده توسط اپراتور GA به صورت زیر می باشد :
تابع برازندگی به صورت معادله 12 در نظر گرفته شده است که باید عملیات بهینه سازی روی آن انجام گیرد.
عموماً در الگوریتم های بهینه سازی استاندارد تابع برازندگی را با نام تابع هدف می شناسند.
سایز جمعیتی که در هر تولید مثل صورت گرفته که البته برای این مقاله کفایت می کند ، 50 می باشد.
بهینه سازی ما همانطور که بیان شد ، شامل دو متغییر می باشد از این رو جمعیت ما می تواند در یک ماتریس قرار بگیرد.
در هر بار تولید مثل و اجرای الگوریتم ژنتیک یک سری محاسبات بر روی جمعیت جاری جهت تولید یک جمعیت جدید صورت می گیرد.
الگوریتم با ایجاد یک جمعیت اولیه تصادفی در بازه [0,2.5] به عنوان رنج اولیه شروع می شود .
در هر مرحله الگوریتم ژنتیک از جمعیت جاری برای تولید فرزندانی که در مرحله بعد قرار است محاسبات رو آنها انجام شود ، استفاده می کند.
در هر مرحله شخص با فیتنس بهتر انتخاب می شود.
بدیهی است که از روش selection استفاده شده است که عموماً روشی قوی و ساده است.
فرزندان زبده و انتخاب شده تعدادی ازافرادی هستند که در تولید مثل جاری ، زنده ماندن آنها تضمین شده است.
تعداد انتخاب ما در هر مرحله حداکثر 5 تا 10 درصد جمعیت اولیه می باشد. ملاک قطع در الگوریتم، رسیدن به جمعیت 300 می باشد.
از میوتیشن گوسین و crossover هیورستیک جهت زاد و ولد برای تولید مثل بعدی استفاده می شود.
همانطور که می دانیم میوتیشن گوسی به دو پارامتر نیازمند است. مقدار میانگین که اغلب معادل صفر است و انحراف معیار در فرایند بهینه سازی می باشد.
Crossover هیورستیک یک فرزندی را بر می گرداند که در راستای خطی قرار دارد که شامل دو والد است که با یک فاصله کوتاه از والد با فیتنس بهتر قرار گرفته است که البته در مسیر مستقیم از والد با فیتنس بد تر قرار دارد.
پارامتر نسبت چگونگی فاصله از والد را می تواند تعیین کند.
معادلات زیر رابطه بین پارامتر نسبت و فرزند در تولید نسل بعدی را نشان می دهد.
Child=parent2+R(parent1-parent2)
کهParent1 و Parent2 والدین هستند و Parent1 والدی با فیتنس بهتر می باشد و R پارامتر نسبت می باشد.
عموماً برای مدل های دینامیکی مرتبه دوم پارامتر نسبت 1.2 در نظر گرفته می شود.
از یک تابع هیبریدی جهت افزایش قدرت الگوریتم ژنتیک استفاده شده است.
تابع هیبریدی یک تابع بهینه سازی می باشد که بعد از توقف الگوریتم ژنتیک اجرا می شود و باعث بهبود مقادیر تابع فیتنس می شود.
تابع هیبریدی از نقطه نهایی الگوریتم ژنتیک به عنوان نقطه اولیه استفاده می کند و این از طریق باعث بهبود مقادیر تابع فیتنس می شود.
ما از تابع fminsearch که یک تابع مینیمم سازی در بهینه سازی است استفاده کرده ایم.
این تابع یک روش جستجوی مستقیم ارائه می دهد که عموماً در محاسبات عددی و تحلیل های گرادیانی مورد استفاده قرار نمی گیرد.
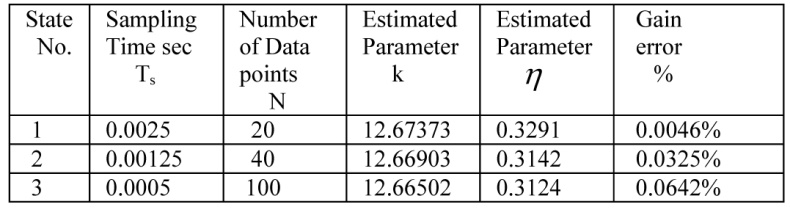
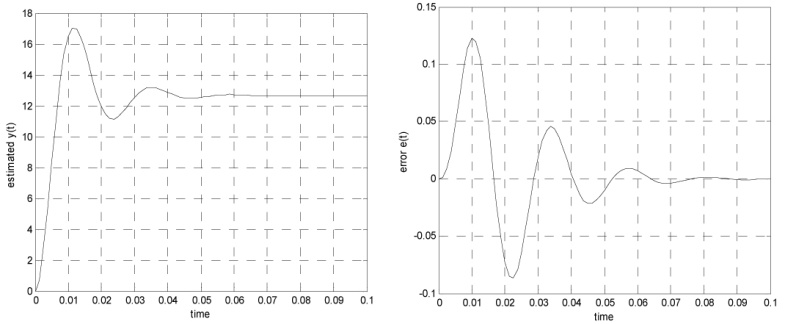
نتایج تخمین بر اساس الگوریتم ژنتیک در جدول 2 گردآوری شده است.
کار انجام شده بر اساس الگوریتم ژنتیک را با روش LSE مقایسه می کنیم.
معادله شماره 9 را در حوزه زمان به صورت زیر می توانیم بنویسیم :
بر اساس روش استفاده شده در مرجع شماره 1 (با در نظر گرفتن ضمیمه) و K بدست خواهد آمد نتایج شبیه سازی بر اساس روش LSE در جدول شماره (3) گرد آوری شده است.
نتایج شبیه سازی
برای تقریب پارامتر ها سه مرحله در نظر گرفته شده است و هر مرحله شامل پارامتر های تخمین زده شده می باشد.
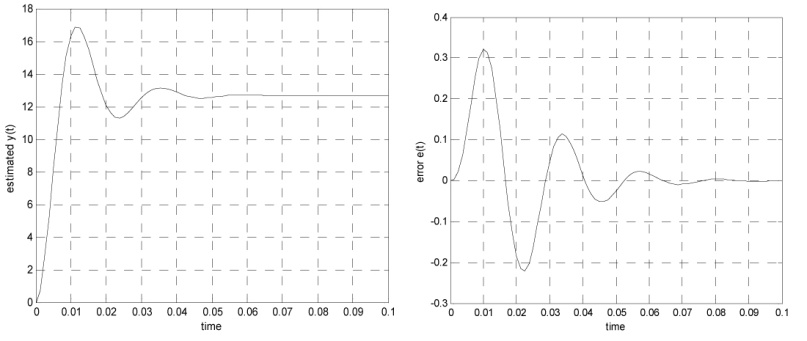
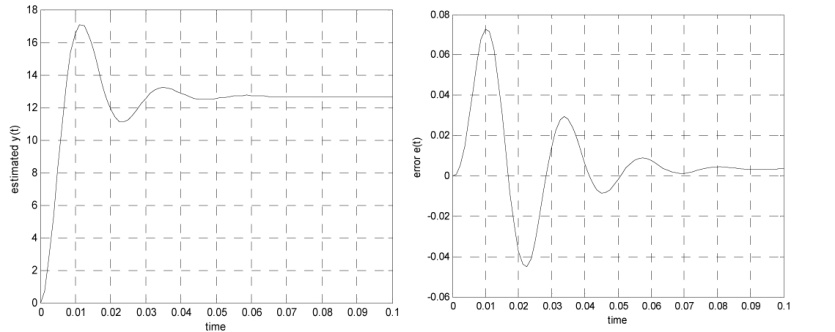
شکل های مدل تخمین زده شده بر اساس تخمین پارامترها و خطای مدل تخمین زده شده و تست موتور بر اساس شکل 4 رسم شده است.
جدول 2 نتایج تقریب بر اساس الگوریتم ژنتیک
شکل 6- مرحله 1 پاسخ پله مدل تخمینی و خطا
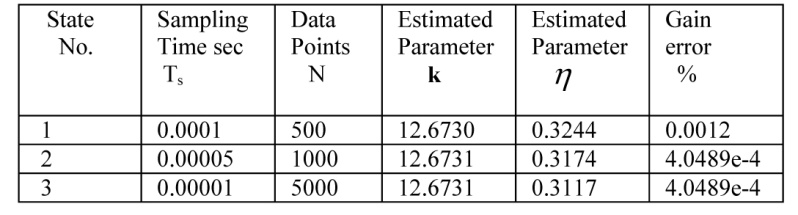
شکل 7- مرحله 2 پاسخ پله مدل تخمینی و نیز خطا
جدول 3 نتایج تقریب بر اساس LSE
شکل 9 مرحله 1 – پاسخ پله مدل تخمینی و نیز خطا
شکل 10- مرحله 2 پاسخ پله مدل تخمینی
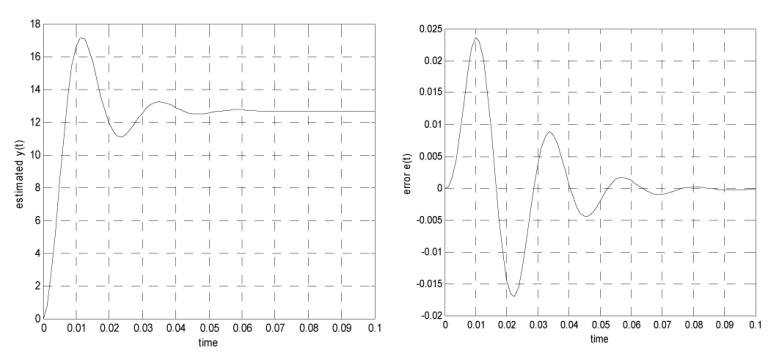
شکل 11- مرحله 3 پاسخ پله مدل تخمینی و نیز خطا
مقایسه ی تخمین بر اساس الگوریتم ژنتیک و تخمین LSE
اختلاف بین تخمین به روش الگوریتم ژنتیک و تخمین به روش حداقل مربعات خطا هنگامی که تعداد داده ها کاهش یابد، مشهود خواهد بود.
نتایج شبیه سازی نشان می دهد که دقت بالا در الگوریتم حداقل مربعات هنگامی حاصل خواهد شد که تعداد نقاط داده ها افزایش یابد و زمان نمونه برداری کاهش یابد.
با تعداد نقاط داده یکسان نتایج حاصل از تخمین بوسیله GA و LSE با تعداد نقاط داده N=20 و N=40 در شکل های 12 و 13 و 14 و 15 نشان داده شده است .
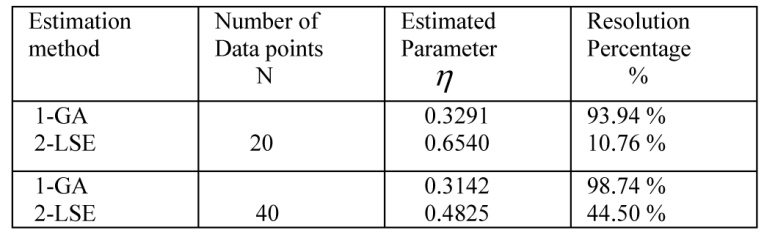
جداول 4و 5 وضوح کار انجام شده از هردو روش را نشان می دهد.
ملاحظه 1- درصد خطای بهره به صورت زیر نشان داده می شود:
ملاحظه2- فاکتور شکل دهی به صورت زیر تعریف می شود :
توجه :
و بهره اصلی در دسترس نیستند اما ما پارامتر های موتور DC که در جدول 1 آمده است را به کار خواهیم برد.
جدول شماره 4 مقایسه میان الگوریتم ژنتیک و روش حداقل خطا برای N=20 , 40
جدول شماره 5 مقایسه دقت دو روش برای N=20,40
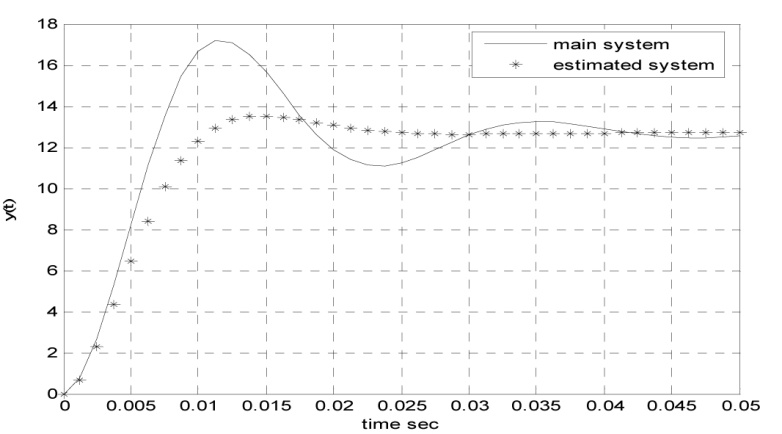
شکل 12 – تخمین بر اساس روش الگوریتم ژنتیک برای N=20 (دقت 93.94%)
شکل 13- تخمین بر اساس روش حداقل مربعات برای N=20 (دقت 10.76%)
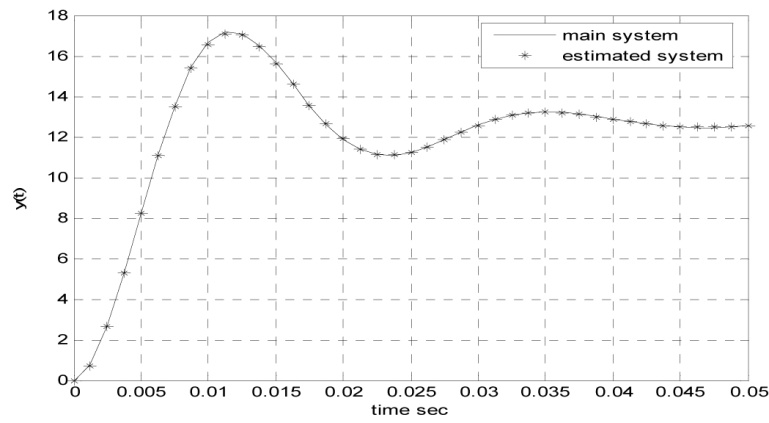
شکل 14- تخمین بر اساس الگوریتم ژنتیک برای N=40 (دقت 98.74%)
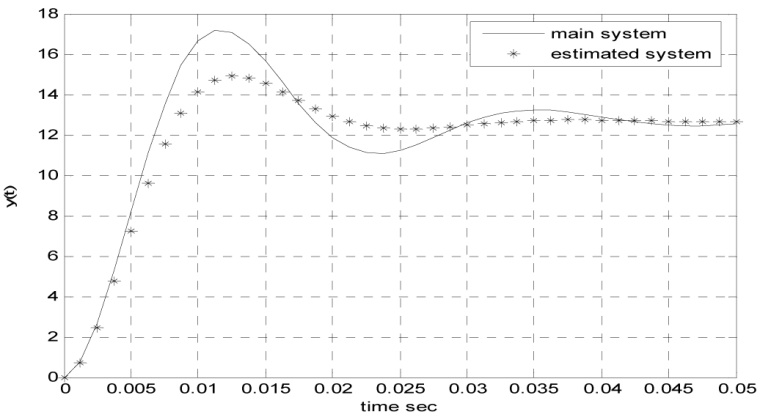
شکل 15- تخمین بر اساس روش حداقل مربعات برای N=40 (دقت 44.5%)
نتیجه گیری :
در این مقاله حالت دینامیک موتور DC با استفاده از دو روش GA وLSE توصیف شده است.
با توجه به توانایی روش بهینه سازی توسط GA در یافتن نقطه بهینه سراسری و نیاز به دقت بالا در تخمین پارامتر ها ، روش پیشنهادی در تخمین offline پارامتر ها GA خواهد بود.
روش GA با تعداد نقاط کمتر همان دقت روش LSE را دارا خواهد بود .
دقت در تخمین پارامتر ها مخصوصاً پارامتر که در شناسایی حالت دینامیکی بسیار مهم می باشد. با این روش امکان پذیر است.
بر خلاف روش LSE روش تخمین پارامتر ها بوسیله GAرا بر همه سیستم های LTI که پارامتر های غیر خطی اند می توان بکار برد.
ضمیمه:
هسته اصلی برنامه انجام شده در مقاله
clc
close all
clear all
T=input(‘enter sampel Time :’)
max=.1/T;
disp(‘ maximom Data point is =’)
M=sprintf(‘%f’, max)
N=input(‘Enter Number of data points(your number must be less than M):’)
save T
save N
aw=120;
options=gaoptimset(‘PopulationSize’,30,’MutationFcn’, @mutationgaussian,’CrossoverFcn’, @crossoverscattered,’Generations’,aw,’StallGenLimit’,50,’StallTimeLimit’,50,’HybridFcn’,@fminsearch);
[x,c] = ga(@susp_ga,2,options );
clc
c
K=x(1)
Z=x(2)
sim(‘Dc_motor’,[0 .1]);
plot(t,y);
title(‘step response of tested motor’);
figure;
plot(t,y1);
title(‘step response of estimated motor’);
figure;
plot(t,y);
hold on;
plot(t,y1,’r’)
legend(‘step response of tested motor’,’step response of estimated motor’);
figure;
plot(t,e);
title(‘error’);
زیر برنامه مربوط به بخش شبیه سازی:
function F = susp_ga(x)
load T
load N
K=x(1);
Z=x(2);
simopt = simset(‘solver’,’ode45′,’SrcWorkspace’,’Current’);
% Initialize sim options
sim(‘Dc_motor’,[0 .1],simopt);
F =sum( (y(1:N)-y1(1:N)).^2 );
در ادامه کار انجام شه توسط خودمان برای توسعه مقاله مذکور را بیان می کنیم :
سیستم ما دارای دو ورودی و دو خروجی می باشد.
ورودی ها ولتاژ و گشتاور بوده و خروجی آن سرعت و جریان ورودی می باشد.
بنابراین سیستم ما دارای 4 تابع تبدیل به صورت زیر می باشد.
برای بدست آوردن داده های مورد نیاز در آزمایشگاه به صورت زیر عمل می کنیم :
داده های مورد نیاز برای بدست آودن تابع تبدیل در صورتیکه ورودی ولتاژ باشد و خروجی سرعت .
در حالت بی باری به موتور یک پله ولتاژ اعمال کرده و سرعت را اندازه گیری می کنیم.
در این حالت باید توجه داشت که چون ولتاژ ناگهانی به موتور اعمال شده است دامنه جریان ورودی زیاد می باشد ، بنابراین باید ولتاژ ورودی به اندازه ای باشد که جریان از جریان نامی موتور فراتر نرود.
داده های مورد نیاز برای بدست آودن تابع تبدیل در صورتیکه ورودی ولتاژ باشد و خروجی جریان.
در حالت بی باری به موتور یک ورودی پله ولتاژ اعمال کرده و جریان را اندازه گیری می کنیم.
داده های مورد نیاز برای بدست آودن تابع تبدیل در صورتیکه ورودی گشتاور باشد و خروجی جریان.
ابتدا موتور را به یک ژنراتور DC کوپل می کنیم. نوع ژنراتور DC تحریک مستقل می باشد.
برای اعمال یک پله گشتاور به موتور ، به ژنراتور یک بار مقاومتی وصل می کنیم.
با وصل شدن بار مقاومتی یک گشتاور مقاوم به محور ژنراتور اعمال شده و چون موتور و ژنراتور به یکدیگر کوپل می باشند، گشتاور به موتور نیز اعمال می شود.
در این حالت باید جریان ورودی موتور را اندازه گیری نماییم.
داده های مورد نیاز برای بدست آودن تابع تبدیل در صورتیکه ورودی گشتاور باشد و خروجی سرعت .
مانند حالت قبل عمل کرده و این بار سرعت را اندازه گیری می کنیم.
در زیر نمودار های پاسخ سیستم به ورودی های مختلف را می توانید مشاهده کرده و پاسخ ناشی از تابع تبدیل نیز به روش GA برای مقایسه در روی همان نمودار رسم شده است :
شکل 1: پاسخ پله در صورتیکه ورودی گشتاور باشد و خروجی جریان
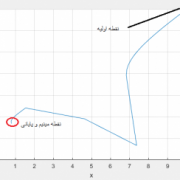
شکل 2: پاسخ پله در صورتیکه ورودی گشتاور باشد و خروجی سرعت
شکل 3: پاسخ پله در صورتیکه ورودی ولتاژ باشد و خروجی جریان آرمیچر
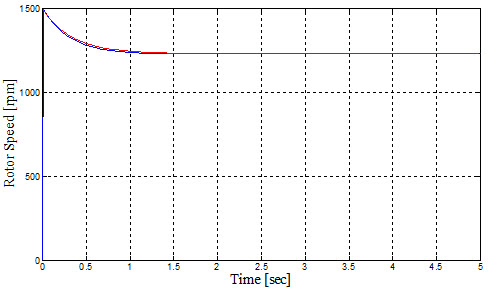
شکل 4: پاسخ پله در صورتیکه ورودی ولتاژ باشد و خروجی سرعت روتور
با توجه به شکل های بالا توابع تبدیل پیشنهاد شده به صورت زیر می باشند:
برای بدست آوردن ضرایب هر کدام از توابع تبدیل بایستی یک منحنی را بر منحنی بدست آمده از نتایج آزمایشگاهی برازش نمود.
با توجه به مزایای روش GA که در بالا بیان شد در برابر LSE در این پروژه از GA برای برازش منحنی استفاده شده است.
برنامه اصلی شامل چهار زیر برنامه و دو فایل شبیه سازی می باشد.
با اجرای برنامه اصلی در هر مرحله زیر برنامه های مربوط به هر تابع تبدیل فراخوانی شده ، نتایج آزمایشگاهی در برنامه بارگزاری شده و شبیه سازی مربوطه انجام می شود.
منحنی حاصل از نتایج شبیه سازی بایستی بر منحنی حاصل از نتایج آزمایشگاهی منطبق باشد.
این کار با تغییر پارامتر های تابع تبدیل توسط الگوریتم ژنتیک و تعریف تابع هدف به صورت مجموع مربعات خطا در هر نقطه شبیه سازی برای نتایج حاصل از شیبه سازی و نتایج آزمایشگاهی انجام خواهد شد.
در پایان یادآوری می شود :
ابزار استفاده شده در آزمایشگاه برای نمونه برداری از ولتاژ و جریان دستگاه Power Analyzer می باشد.
این دستگاه از طریق پورت سریال به کامپیوتر متصل می شود ، نرم افزار مربوط به این دستگاه که در زیر شکل آن را مشاهده می نمایید به همراه دستگاه ارائه می گردد.
هسته اصلی برنامه قسمت توسعه داده شده توسط خودمان :
clc
close all
clear all
disp(‘******************************************************************************************’)
disp(‘In this part VOLTAGE is a input and VELOCITY is a output’)
disp(‘ z ‘)
disp(‘H(s)=————- ‘)
disp(‘ p1*s+p2 ‘)
aw=100;
options = gaoptimset(‘display’,[],’PopulationSize’,50,’MutationFcn’, @mutationgaussian,’CrossoverFcn’, @crossoverscattered,’Generations’,aw,’StallGenLimit’,50,’StallTimeLimit’,100,’HybridFcn’,@fminsearch);
[x,c] = ga(@GAVW,3,options );
z=x(1)
p1=x(2)
p2=x(3)
sim(‘Step_res2’,[0 5]);
figure(1)
plot(Res(:,1),Res(:,2));
load VW
hold on
plot(Res(1:500,1),w(1:500),’red’)
disp(‘******************************************************************************************’)
disp(‘In this part TORQUE is a input and CURRENT is a output’)
disp(‘ z ‘)
disp(‘H(s)=————- ‘)
disp(‘ p1*s+p2 ‘)
aw=100;
options = gaoptimset(‘PopulationSize’,50,’MutationFcn’, @mutationgaussian,’CrossoverFcn’, @crossoverscattered,’Generations’,aw,’StallGenLimit’,50,’StallTimeLimit’,100,’HybridFcn’,@fminsearch);
[x,c] = ga(@GATI,3,options );
z=x(1)
p1=x(2)
p2=x(3)
sim(‘Step_res2’,[0 5]);
figure(2)
plot(Res(:,1),Res(:,2));
load TI
hold on
plot(Res(1:500,1),I(1:500),’red’)
disp(‘******************************************************************************************’)
disp(‘In this part VOLTAGE is a input and CURRENT is a output’)
disp(‘ z1*s+z2 ‘)
disp(‘H(s)=————— ‘)
disp(‘ S^2+p1*S+p2 ‘)
aw=100;
options = gaoptimset(‘PopulationSize’,50,’MutationFcn’, @mutationgaussian,’CrossoverFcn’, @crossoverscattered,’Generations’,aw,’StallGenLimit’,50,…
‘StallTimeLimit’,100,’HybridFcn’,@fminsearch);
[x,c] = ga(@GAVI,5,options );
z1=x(1)
z2=x(2)
p1=x(4)
p2=x(5)
sim(‘Step_res3’,[0 5]);
figure(3)
plot(Res3(:,1),Res3(:,2));
load VI
hold on
plot(Res3(1:500,1),I(1:500),’red’)
disp(‘******************************************************************************************’)
disp(‘In this part TORQUE is a input and VELOCITY is a output’)
disp(‘ z1*s+z2 ‘)
disp(‘H(s)=————— ‘)
disp(‘ S^2+p1*S+p2 ‘)
aw=20;
options = gaoptimset(‘PopulationSize’,50,’MutationFcn’, @mutationgaussian,’CrossoverFcn’, @crossoverscattered,’Generations’,aw,’StallGenLimit’,…
50,’StallTimeLimit’,100,’HybridFcn’,@fminsearch,’TolFun’,1e-10);
[x,c] = ga(@GATW,5,options );
z1=x(1)
z2=x(2)
p1=x(4)
p2=x(5)
simopt = simset(‘solver’,’ode23s’,’SrcWorkspace’,’Current’);
sim(‘Step_res3’,[0 5],simopt);
figure(4)
plot(Res3(:,1),Res3(:,2));
load TW
w(0,0)=0;
hold on
plot(Res3(1:500,1),w(1:500),’red’)
زیر برنامه شماره 1: مربوط به تابع تبدیل شماره 1 – ورودی ولتاژ –خروجی سرعت
function F = VW(x)
load VW
z=x(1);
p1=x(2);
p2=x(3);
simopt = simset(‘solver’,’ode23s’,’SrcWorkspace’,’Current’);
sim(‘Step_res2’,[0 5],simopt);
F =sum((Res(1:500,2)-w(1:500)).^2);
زیر برنامه شماره 2 – ورودی ولتاژ و خروجی جریان
function F = VI(x)
load VI
%
% K=x(1);
% Z=x(2);
% wn=x(3);
z1=x(1);
z2=x(2);
% z3=x(3);
p1=x(4);
p2=x(5);
% p3=x(6);
simopt = simset(‘solver’,’ode45′,’SrcWorkspace’,’Current’);
% Initialize sim options
% sim(‘Step_res’,[0 1],simopt);
sim(‘Step_res3’,[0 5],simopt);
F =sum((Res3(1:500,2)-I(1:500)).^2);
زیر برنامه شماره 3 – ورودی گشتاور – خروجی سرعت
function F = TW(x)
load TW
w(1,1)=0;
z1=x(1);
z2=x(2);
p1=x(4);
p2=x(5);
simopt = simset(‘solver’,’ode23s’,’SrcWorkspace’,’Current’);
% Initialize sim options
% sim(‘Step_res’,[0 1],simopt);
sim(‘Step_res3’,[0 5],simopt);
F =sum((Res3(1:500,2)-w(1:500)).^2);
زیر برنامه شماره 4- ورودی گشتاور و خروجی جریان
function F = TI(x)
load TI
z=x(1);
p1=x(2);
p2=x(3);
simopt = simset(‘solver’,’ode45′,’SrcWorkspace’,’Current’);
% Initialize sim options
% sim(‘Step_res’,[0 1],simopt);
sim(‘Step_res2’,[0 5],simopt);
F =sum((Res(1:500,2)-I(1:500)).^2);
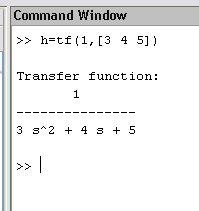
خروجی های برنامه در پنجره command
****************************************************************************In this part VOLTAGE is a input and VELOCITY is a output
z
H(s)=————-
p1*s+p2
Optimization terminated: average change in the fitness value less than options.TolFun.
z =
11.4848
p1 =
0.0111
p2 =
0.0153
****************************************************************************
In this part TORQUE is a input and CURRENT is a output
z
H(s)=————-
p1*s+p2
Optimization terminated: average change in the fitness value less than options.TolFun.
z =
0.9221
p1 =
0.0334
p2 =
0.1094
****************************************************************************
In this part VOLTAGE is a input and CURRENT is a output
z1*s+z2
H(s)=—————
S^2+p1*S+p2
Optimization terminated: maximum number of generations exceeded.
z1 =
339.7156
z2 =
14.0418
p1 =
11.5382
p2 =
26.3814
****************************************************************************
In this part TORQUE is a input and VELOCITY is a output
z1*s+z2
H(s)=—————
S^2+p1*S+p2
Optimization terminated: maximum number of generations exceeded.
z1 =
3.6132
z2 =
1.4062
p1 =
-1.0285
p2 =
-0.3210
پاسخ پله جریان آرمیچر به گشتاور ناشی از نتایج آزمایشگاهی و تابع تبدیل بدست آمده از الگوریتم ژنتیک (قرمز نتایج آزمایشگاهی و آبی خروجی الگوریتم ژنتیک)
پاسخ پله سرعت روتور به گشتاور ناشی از نتایج آزمایشگاهی و تابع تبدیل بدست آمده از الگوریتم ژنتیک (قرمز نتایج آزمایشگاهی و آبی خروجی الگوریتم ژنتیک)
پاسخ پله جریان آرمیچر به ولتاژ ورودی از نتایج آزمایشگاهی و تابع تبدیل بدست آمده از الگوریتم ژنتیک (قرمز نتایج آزمایشگاهی و آبی خروجی الگوریتم ژنتیک)
پاسخ پله سرعت روتور به ولتاژ ورودی ناشی از نتایج آزمایشگاهی و تابع تبدیل بدست آمده از الگوریتم ژنتیک (قرمز نتایج آزمایشگاهی و آبی خروجی الگوریتم ژنتیک)



















دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.