حل تابع با سری تیلور و روش نیوتن در متلب
حل تابع با سری تیلور و روش نیوتن در متلب
دستور متلب
syms x
g=1/(x^3-(3/4)*x-0.5);
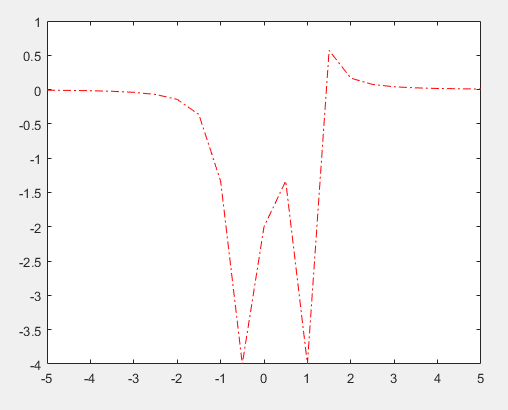
شکل خودتابع
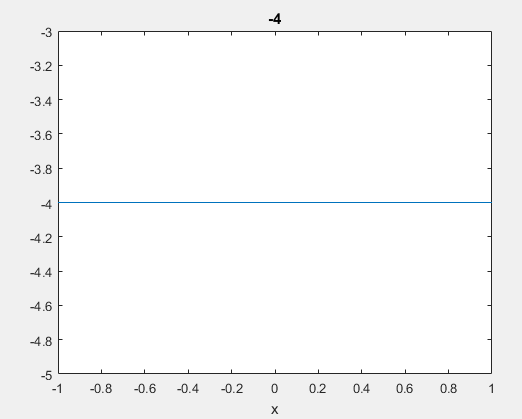
t1=taylor(g, x,-0.5, ‘Order’, 2);
t1=-4
ezplot(t1,[-1,1]);hold on
شکل بسط تیلور مرتیه دوم در نقطه 0.5-
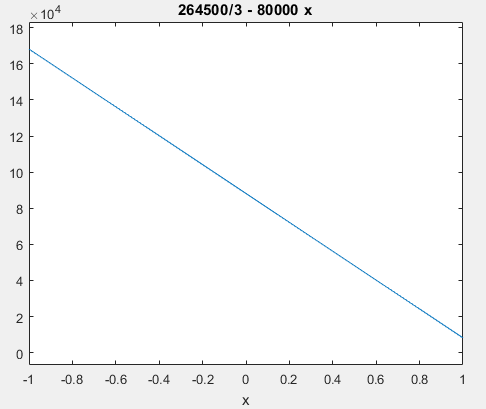
t2=taylor(g, x,1.1, ‘Order’, 2);
==============================================
t2 =
264500/3 – 80000*x
ezplot(t2,[-1,1]);
نمودار بسط تیلور تابع در نقطه 1.1
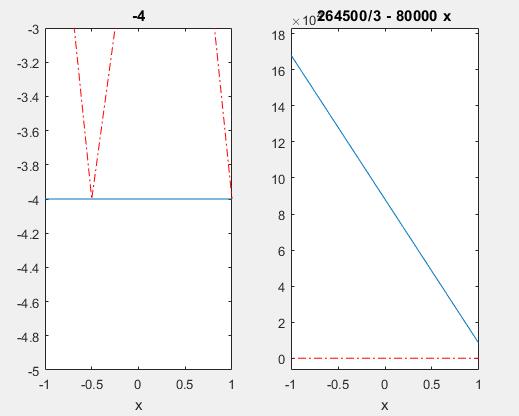
نمودار قرمز تابع اصلی بوده و نمودار ابی رنگ مربوط به هریک از بسطهای تیلور در دو نقطه مختلف می باشد. طبق ان جیزی که دیده می شود اختلاف بین این تابع اصلی و تابع بسط تیلور درجه دوم داده شده خیلی زیاد می باشد.
Theorem 2: Consider a differentiable function . Suppose at a point we have:
(a) then is a STATIONARY point (and of special interest in optimization).
(b) and then the function takes a MINIMA at x = x*
(c) and then the function takes a MAXIMA at x = x*
طبق این قضیه ریشه های مشتق اول تابع یک نقطه stationary می باشد که یا مینیم محلی می باشد یا ماکزیمم محلی
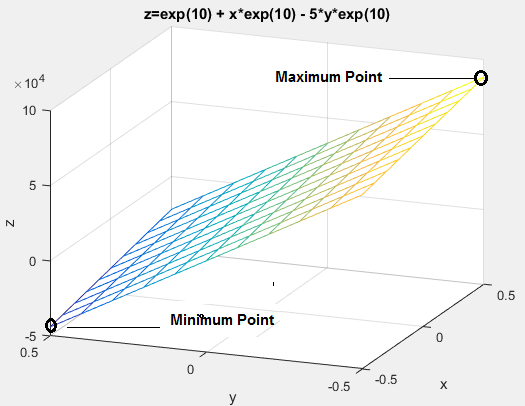
[x1,x2]=meshgrid(-0.5:0.1:0.5,-0.5:0.1:0.5)
z=exp(10) + x1*exp(10) – 5*x2*exp(10);
mesh(x1,x2,z)
دو نقطه طبق شکل نقطه stationary می باشد. (0.5و0.5-) نقطه مینیم تابع می باشد و (0.5-و0.5) نقطه ماکزیمم تابع می باشد.
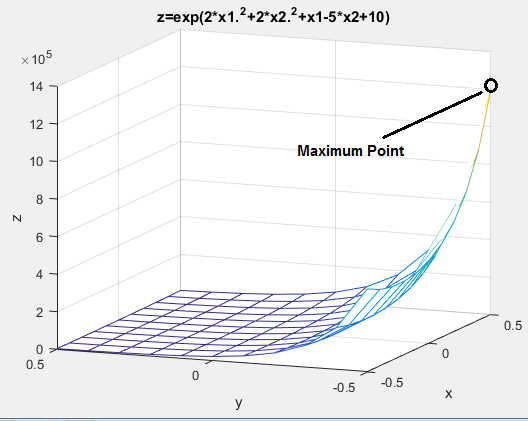
شکل زیر منحنی درجه دوم تابع اصلی می باشد که دارای یک نقطه ماکزیمم و بی نهایت نقطه می نیمم می باشد
. نقطه (0.05-و0.5) یک نقطه ماکزیمم بوده و یکی از نقاط می نیممم( 0.5و0.5-) می باشد.که هردو نقاط stationary تابع می باشد.
هردو نقاط در دوتابع اصلی و تابع تقریب زده شده یکی می باشد.
%==============================================%
%initialization مقدار دهی اولیه
a=[-1 1]
b=[1 1]
%================================================
%Dsfine Function تعریف خود تابع
syms x1 x2
f=3.5*x^2-6*x1*x2-x2^2; تابع گزینه الف
X=[x1 x2]
%====================================================
%First Directional Derivative مشتق جهت دار درجه اول
g=gradient(f,X)
dd=(a/sqrt(a(1)^2+a(2)^2))*g
s=subs(dd,X,b)
s1=double(s) مقدار مشتق جهت دار درجه اول
%=========================================================
%Secend Directional Derivative مشتق جهت دار درجه دوم
gg=gradient(dd,X)
v=(a/sqrt(a(1)^2+a(2)^2))*gg;
ss=subs(v,X,b)
s2=double(ss) مقدار مشتق جهت دار درجه دوم
%==============================================%
%initialization مقدار دهی اولیه
a=[-1 1]
b=[1 1]
%================================================
%Dsfine Function تعریف خود تابع
syms x1 x2
f=5*x^2-6*x1*x2+5*x2^2+4*x1+4*x2; تابع گزینه الف
X=[x1 x2]
%====================================================
%First Directional Derivative مشتق جهت دار درجه اول
g=gradient(f,X)
dd=(a/sqrt(a(1)^2+a(2)^2))*g
s=subs(dd,X,b)
s1=double(s) مقدار مشتق جهت دار درحه اول
%=========================================================
%Secend Directional Derivative مشتق جهت دار درجه دوم
gg=gradient(dd,X)
v=(a/sqrt(a(1)^2+a(2)^2))*gg;
ss=subs(v,X,b)
s2=double(ss) مقدار مشتق جهت دار درجه دوم
%==============================================%
%initialization مقدار دهی اولیه
a=[-1 1]
b=[1 1]
%================================================
%Dsfine Function تعریف خود تابع
syms x1 x2
f=4.5*x^2-2*x1*x2+3*x2^2+2*x1-1*x2; تابع گزینه الف
X=[x1 x2]
%====================================================
%First Directional Derivative مشتق جهت دار درجه اول
g=gradient(f,X)
dd=(a/sqrt(a(1)^2+a(2)^2))*g
s=subs(dd,X,b)
s1=double(s) مقدار مشتق جهت دار درحه اول
%=========================================================
%Secend Directional Derivative مشتق جهت دار درجه دوم
gg=gradient(dd,X)
v=(a/sqrt(a(1)^2+a(2)^2))*gg;
ss=subs(v,X,b)
s2=double(ss) مقدار مشتق جهت دار درجه دوم
%==============================================%
%initialization مقدار دهی اولیه
a=[-1 1]
b=[1 1]
%================================================
%Dsfine Function تعریف خود تابع
syms x1 x2
f=-0.5*(7*x^2+12*x1*x2+-2*x2^2); تابع گزینه الف
X=[x1 x2]
%====================================================
%First Directional Derivative مشتق جهت دار درجه اول
g=gradient(f,X)
dd=(a/sqrt(a(1)^2+a(2)^2))*g
s=subs(dd,X,b)
s1=double(s) مقدار مشتق جهت دار درحه اول
%=========================================================
%Secend Directional Derivative مشتق جهت دار درجه دوم
gg=gradient(dd,X)
v=(a/sqrt(a(1)^2+a(2)^2))*gg;
ss=subs(v,X,b)
s2=double(ss) مقدار مشتق جهت دار درجه دوم
%=====================================================
syms x
f=x^4-0.5*x^2+1; تعریف تابع
%====================================================
f1=diff(f); مشتق تابع حهت بدست اوردن ریشه ها
pretty(f1)
%======================================================
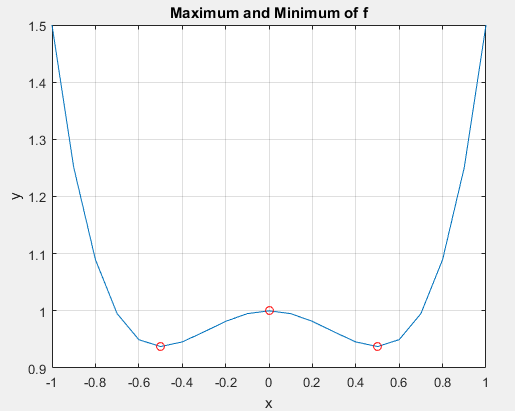
crit_pts = solve(f1) نقاط اکسترمم تابع
%====================================================
xd=-1:0.1:1;
yd=subs(f,x,xd);
plot(xd,yd);
hold on
plot(double(crit_pts), double(subs(f,crit_pts)),’ro’);
title(‘Maximum and Minimum of f’);
text(-4.8,5.5,’Local minimum’);
text(-2,4,’Local maximum’)
hold off;
grid
xlabel(‘x’);ylabel(‘y’)
نفاط اکسترمم بدست امده بعد اجرای برنامه
(a) then is a STATIONARY point (and of special interest in optimization).
(b) and then the function takes a MINIMA at x = x*
(c) and then the function takes a MAXIMA at x = x*
syms x1 x2
f=(x1+x2)^4-12*x1*x2+x1+x2+1
g=gradient(f,[x1,x2])
S=solve(‘ 4*(x1 + x2)^3 – 12*x2 + 1′,’ 4*(x1 + x2)^3 – 12*x1 + 1′)
S=[S.x1 S.x2];
S=double(S)
این سه نقطه دقیقا همان سه نقطه بالایی هستند که از خروجی برنامه بدست امد. حال برای تشخیص اینکه کدام ماکزیمم و کدام مینیم و یا کدام زینی هست به طریق زیر عمل میکنیم
هسیان تابع به صورت زیر می باشد
syms x1 x2
f=(x1+x2)^4-12*x1*x2+x1+x2+1
g=gradient(f,[x1,x2])
S=solve(‘ 4*(x1 + x2)^3 – 12*x2 + 1′,’ 4*(x1 + x2)^3 – 12*x1 + 1′)
S=[S.x1 S.x2];
S=double(S)
h=hessian(f,[x1,x2])
AP1=double(h,[x1,x2], S(1,:)) بررسی نقطه اول
AP2=double(h,[x1,x2], S(2,:))بررسی نقطه دوم
AP3=double(h,[x1,x2], S(3,:)) بررسی نقطه سوم
برای بررسی نقطه (0.5655و0.5655) باید چهارپارامترA,B,C,D را حساب کنیم نقطه AP1 این ماتریس را نشان میدهد.طبق زیر هر جهارتا مثبت می باشد. دلتا برای این ماتریس برابر است با منفی دترمینان ماترس هسیان تابع که برابر است با 224.3328- که یک عدد منفی می باشد بناربراین نقطه بالایی مینیمم نسبی تابع می باشد.
برای بررسی نقطه (0.6504-و0.6504-) باید چهارپارامترA,B,C,D را حساب کنیم نقطه AP2 این ماتریس را نشان میدهد.طبق زیر هر جهارتا مثبت می باشد. دلتا برای این ماتریس برابر است با منفی دترمینان ماترس هسیان تابع که برابر است با .343.4389- که یک عدد منفی می باشد بناربراین نقطه بالایی مینیمم نسبی تابع می باشد.
برای بررسی نقطه (0.850و0.850) باید چهارپارامترA,B,C,D را حساب کنیم نقطه AP3 این ماتریس را نشان میدهد.طبق زیر پارامتر Aر مثبت می باشد. دلتا برای این ماتریس برابر است با منفی دترمینان ماترس هسیان تابع که برابر است با .135.6828 که یک عدد مثبت می باشد بناربراین نقطه بالایی نقطه زینی تابع می باشد.
پیدا کردن مقادیر سری تیلور در سه نقطه
t1=(taylor(f, [x1,x2],S(1,:), ‘Order’, 2));
t1=subs(t1,[x1,x2],S(1,:));
t1=double(t1)
t2=(taylor(f, [x1,x2],S(2,:), ‘Order’, 2));
t2=subs(t2,[x1,x2],S(2,:));
t2=double(t2)
t3=(taylor(f, [x1,x2],S(3,:), ‘Order’, 2));
t3=subs(t3,[x1,x2],S(3,:));
t3=double(t3)
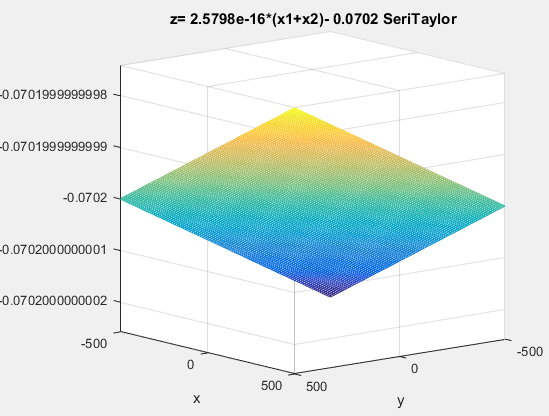
نمودار بسط تیلور به صورت یک صفحه می باشد که به صورت زیر است
clc
clear
%fx=cx-sum(log(b-ax)) m=100, n=20
P= [ 6 -2
-2 6];
q=[-1
-1];
r=0;
n=size(P,1)
x=[0 ;0]
%—————————Fx
Fx=0.5*x’*P*x+q’*x+r
%—————————Grad_Fx
Grad_Fx=P*x+q
g=0;
for j=1:n
if abs(Grad_Fx(j,1))>g
g=abs(Grad_Fx(j,1));
co=j
end
end
%————————-
jj=1;
fx(jj)=Fx
x1(jj,:)=x;
cc(jj)=jj
ng(jj)=norm(Grad_Fx);
while norm(Grad_Fx)>0.01
t=1
alpha=0.6
beta=.95
e=zeros(n,1);
e(co)=1;
Delta_x=-(Grad_Fx).*e
y=x+t.*Delta_x
%————————-Fx(x+t.dita_x)
Fy=0.5*y’*P*y+q’*y+r
%————————backtracking
while 0.5*y’*P*y+q’*y+r>0.5*x’*P*x+q’*x+r+alpha.*t.*Grad_Fx’*Delta_x
t=beta.*t;
y=x+t.*Delta_x
jj
tt(jj)=t
end
%———————————updating: x
x=x+t.*Delta_x
%———————————updating: f(x) and gradient
Fx=0.5*x’*P*x+q’*x+r
%—————————Grad_Fx
Grad_Fx=P*x+q
g=0;
for j=1:n
if abs(Grad_Fx(j,1))>g
g=abs(Grad_Fx(j,1));
co=j
end
end
%———————————
jj=jj+1;
cc(jj)=jj
fx(jj)=Fx
x1(jj,:)=x;
ng(jj)=norm(Grad_Fx)
end
Grad_Fx
cc
x1
fx
%plot(cc,log10(fx))
plot(x1(:,1),x1(:,2),’r-o’)
[X1,X2]=meshgrid(-0.4:0.01:0.4,-0.4:0.01:0.4);
f=3*X1.^2+3*X2.^2-2*X1*X2-X1-X2;
hold on
contour(X1,X2,f)
xlabel(‘x’);ylabel(‘y’)
grid
clc
clear
a=2;b=2
x=[a; b]’%4.*ones(n,1)
%—————————
syms x1 x2 y1 y2
Fxx=9*x1^4+4*x2^4-90*x1^3-40*x2^3+6*x1^3*x2+8*x1*x2^3-11*x1^2*x2^2+236*x1^2+106*x2^2+30*x1^2*x2+80*x1*x2^2+303*x1*x2-20*x1-20*x2+52;
Grad_Fx=gradient(Fxx,[x1,x2]);
Hs_Fx=hessian(Fxx,[x1,x2]);
%—————————
x=[a;b]
Fx=double(subs(Fxx,[x1,x2],[a,b]))
Grad_Fx=double(subs(Grad_Fx,[x1,x2],[a,b]));
Hs_Fx=double(subs(Hs_Fx,[x1,x2],[a,b]))
%————————-
jj=1;
fx(jj)=Fx
xx1(jj,:)=x;
cc(jj)=jj
ng(jj)=norm(Grad_Fx);
while ng(jj)>0.001
t=1
alpha=0.8
beta=0.1
Delta_x=-inv(Hs_Fx)*Grad_Fx;
y=x+t*Delta_x
c=y(1);d=y(2);
%————————-
Fyy=9*y1^4+4*y2^4-90*y1^3-40*y2^3+6*y1^3*y2+8*y1*y2^3-11*y1^2*y2^2+236*y1^2+106*y2^2+30*y1^2*y2+80*y1*y2^2+303*y1*y2-20*y1-20*y2+52;
Fy=double(subs(Fyy,[y1,y2],[c,d]))
%————————backtracking
while Fy>Fx+alpha.*t.*Grad_Fx’*Delta_x
t=beta.*t;
y=x+t.*Delta_x
c=y(1);d=y(2);
Fy=double(subs(Fyy,[y1,y2],[c,d]))
jj
tt(jj)=t
end
%———————————updating: x
x=x+t.*Delta_x
a=x(1);b=x(2)
%———————————updating: f(x) and gradient
% Fx=9*x1^4+4*x2^4-90*x1^3-40*x2^3+6*x1^3*x2+8*x1*x2^3-11*x1^2*x2^2+236*x1^2+106*x2^2+30*x1^2*x2+80*x1*x2^2+303*x1*x2-20*x1-20*x2+52;
%—————————
Grad_Fx=gradient(Fxx,[x1,x2]);
Hs_Fx=hessian(Fxx,[x1,x2]);
Fx=double(subs(Fxx,[x1,x2],[a,b]));
Grad_Fx=double(subs(Grad_Fx,[x1,x2],[a,b]));
Hs_Fx=double(subs(Hs_Fx,[x1,x2],[a,b]));
%———————————
jj=jj+1;
cc(jj)=jj
fx(jj)=Fx
xx1(jj,:)=x;
ng(jj)=norm(Grad_Fx)
end
Grad_Fx
cc
xx1
fx
hold on
%plot(cc,log10(fx))
hold on
plot(xx1(:,1),xx1(:,2))
grid
xlabel(‘x’);ylabel(‘y’)
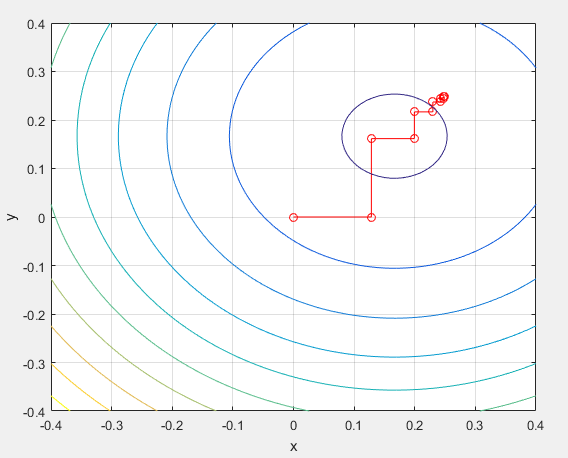
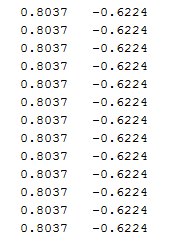
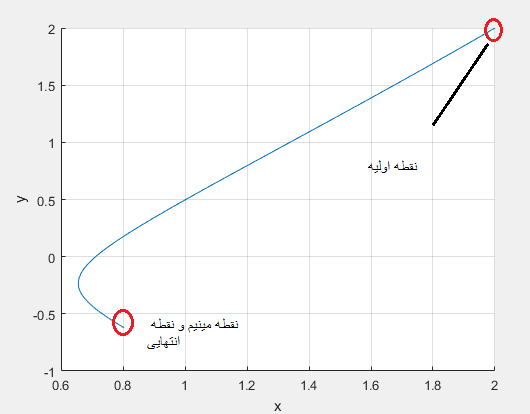
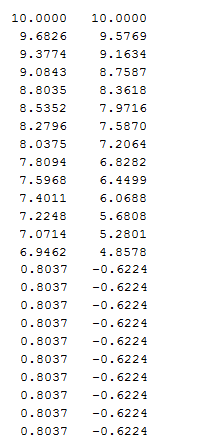
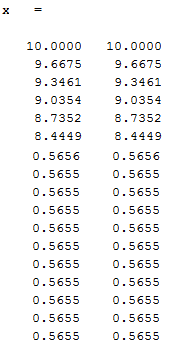
خروجی برنامه به شکل زیر است که با نقطه شروع مختلف با دو تکرار به جواب رسیده است.نقطه زیر نقطه بهینه و تابع را در نقطه بهینه نشان می دهد.
X0=[2,2]
X=
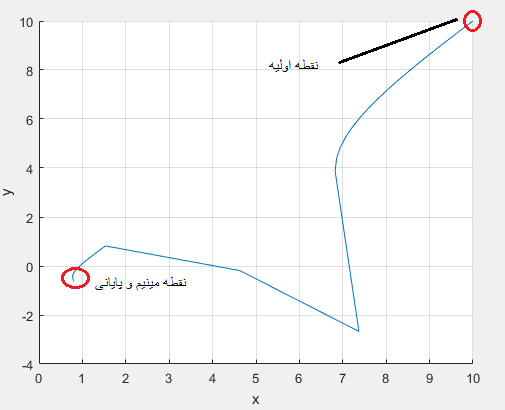
X0=[10,10]
X=
روش نیوتن
clc
clear
a=10;b=10
x=[a; b]’%4.*ones(n,1)
%—————————
syms x1 x2 y1 y2
Fxx=x1^4+x2^4+4*x1^3*x2+4*x1*x2^3+6*x1^2*x2^2-12*x1*x2+x1+x2+1;
Grad_Fx=gradient(Fxx,[x1,x2]);
Hs_Fx=hessian(Fxx,[x1,x2]);
%—————————
x=[a;b]
Fx=double(subs(Fxx,[x1,x2],[a,b]))
Grad_Fx=double(subs(Grad_Fx,[x1,x2],[a,b]));
Hs_Fx=double(subs(Hs_Fx,[x1,x2],[a,b]))
%————————-
jj=1;
fx(jj)=Fx
xx1(jj,:)=x;
cc(jj)=jj
ng(jj)=norm(Grad_Fx);
while ng(jj)>0.001
t=1
alpha=0.8
beta=0.1
Delta_x=-inv(Hs_Fx)*Grad_Fx;
y=x+t*Delta_x
c=y(1);d=y(2);
%————————-
Fyy=y1^4+y2^4+4*y1^3*y2+4*y1*y2^3+6*y1^2*y2^2-12*y1*y2+y1+y2+1;
Fy=double(subs(Fyy,[y1,y2],[c,d]))
%————————backtracking
while Fy>Fx+alpha.*t.*Grad_Fx’*Delta_x
t=beta.*t;
y=x+t.*Delta_x
c=y(1);d=y(2);
Fy=double(subs(Fyy,[y1,y2],[c,d]))
jj
tt(jj)=t
end
%———————————updating: x
x=x+t.*Delta_x
a=x(1);b=x(2)
%———————————updating: f(x) and gradient
% Fx=9*x1^4+4*x2^4-90*x1^3-40*x2^3+6*x1^3*x2+8*x1*x2^3-11*x1^2*x2^2+236*x1^2+106*x2^2+30*x1^2*x2+80*x1*x2^2+303*x1*x2-20*x1-20*x2+52;
%—————————
Grad_Fx=gradient(Fxx,[x1,x2]);
Hs_Fx=hessian(Fxx,[x1,x2]);
Fx=double(subs(Fxx,[x1,x2],[a,b]));
Grad_Fx=double(subs(Grad_Fx,[x1,x2],[a,b]));
Hs_Fx=double(subs(Hs_Fx,[x1,x2],[a,b]));
%———————————
jj=jj+1;
cc(jj)=jj
fx(jj)=Fx
xx1(jj,:)=x;
ng(jj)=norm(Grad_Fx)
end
Grad_Fx
cc
xx1
fx
hold on
%plot(cc,log10(fx))
hold on
plot(xx1(:,1),xx1(:,2))
grid
xlabel(‘x’);ylabel(‘y’)
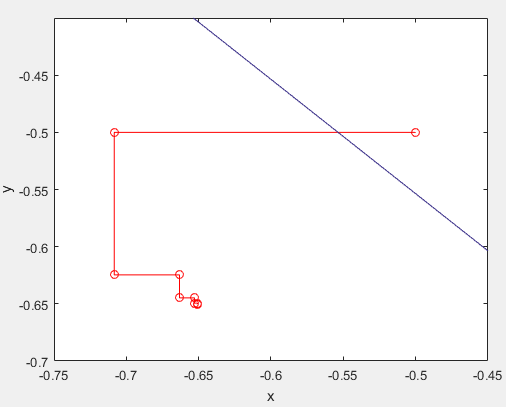
روش کاهشی تند steepest descent
clc
clear
%fx=cx-sum(log(b-ax)) m=100, n=20
a=-0.5;b=-0.5
x=[a; b]’%4.*ones(n,1)
n=2;
%—————————
syms x1 x2 y1 y2
Fxx=x1^4+x2^4+4*x1^3*x2+4*x1*x2^3+6*x1^2*x2^2-12*x1*x2+x1+x2+1;
Grad_Fx=gradient(Fxx,[x1,x2]);
Hs_Fx=hessian(Fxx,[x1,x2]);
%—————————
x=[a;b]
Fx=double(subs(Fxx,[x1,x2],[a,b]))
Grad_Fx=double(subs(Grad_Fx,[x1,x2],[a,b]));
Hs_Fx=double(subs(Hs_Fx,[x1,x2],[a,b]))
g=0;
for j=1:2
if abs(Grad_Fx(j,1))>g
g=abs(Grad_Fx(j,1));
co=j
end
end
%————————-
jj=1;
fx(jj)=Fx
xx1(jj,:)=x;
cc(jj)=jj
ng(jj)=norm(Grad_Fx);
while norm(Grad_Fx)>0.01
t=1
alpha=0.5
beta=.95
e=zeros(n,1);
e(co)=1;
Delta_x=-(Grad_Fx).*e
y=x+t.*Delta_x
c=y(1);d=y(2);
%————————-
Fyy=y1^4+y2^4+4*y1^3*y2+4*y1*y2^3+6*y1^2*y2^2-12*y1*y2+y1+y2+1;
Fy=double(subs(Fyy,[y1,y2],[c,d]))
%————————backtracking
while Fy>Fx+alpha.*t.*Grad_Fx’*Delta_x
t=beta.*t;
y=x+t.*Delta_x
c=y(1);d=y(2);
Fy=double(subs(Fyy,[y1,y2],[c,d]))
jj
tt(jj)=t
end
%———————————updating: x
x=x+t.*Delta_x
a=x(1);b=x(2)
%———————————updating: f(x) and gradient
% Fx=9*x1^4+4*x2^4-90*x1^3-40*x2^3+6*x1^3*x2+8*x1*x2^3-11*x1^2*x2^2+236*x1^2+106*x2^2+30*x1^2*x2+80*x1*x2^2+303*x1*x2-20*x1-20*x2+52;
%—————————
Grad_Fx=gradient(Fxx,[x1,x2]);
Hs_Fx=hessian(Fxx,[x1,x2]);
Fx=double(subs(Fxx,[x1,x2],[a,b]));
Grad_Fx=double(subs(Grad_Fx,[x1,x2],[a,b]));
Hs_Fx=double(subs(Hs_Fx,[x1,x2],[a,b]));
g=0;
for j=1:n
if abs(Grad_Fx(j,1))>g
g=abs(Grad_Fx(j,1));
co=j
end
end
%———————————
jj=jj+1;
cc(jj)=jj
fx(jj)=Fx
xx1(jj,:)=x;
ng(jj)=norm(Grad_Fx)
end
Grad_Fx
cc
x1
fx
%plot(cc,log10(fx))
plot(xx1(:,1),xx1(:,2),’r-o’)
[x1,x2]=meshgrid(-2:0.1:-0.4,-2:0.1:-0.4);
f=x1^4+x2^4+4*x1^3*x2+4*x1*x2^3+6*x1^2*x2^2-12*x1*x2+x1+x2+1;
hold on
contour(x1,x2,f)
axis([-0.75 -0.45 -0.7 -0.4])
grid
xlabel(‘x’);ylabel(‘y’)
grid
نقطه شروع برابر گرفتیم با (0.5-و0.5-)






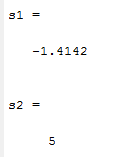
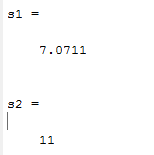
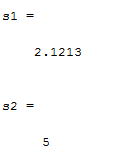
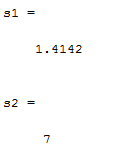


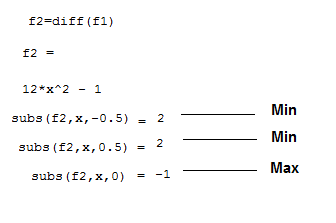

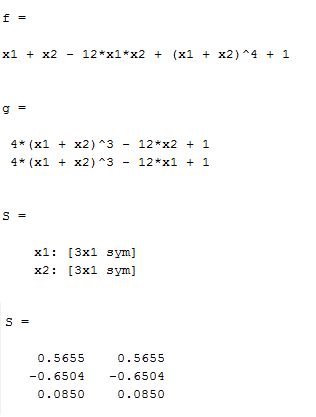

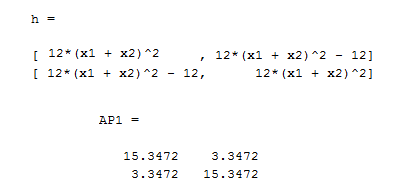
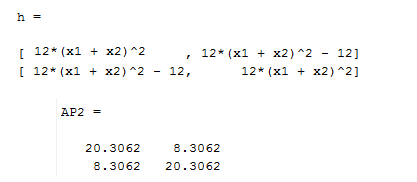
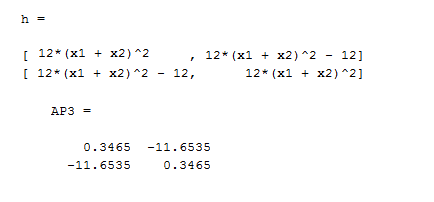
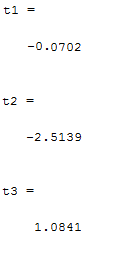








دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.