ماشین های القایی متقارن در متلب
نظریه ماشین های القایی متقارن در متلب
analysis of electric machinery exercises in Matlab
برای شبیه سازی یک موتور القایی در متلب روشهای گوناگونی می تواند مطرح باشد, از آنجایی که معادلات حاکم بر این موتورها در اختیار است, می توانیم با انتگرال گیری عددی به جوابهای قابل قبولی برسیم.
در ابتدا با استفاده از الگوریتم انتگرال گیری رانگ کوتاه معادلات موتور القایی دلخواهی را در فضای مرجع دلخواه با متلب شبیه سازی کرده و نتایج را مشاهده می کنیم.
clear all
clc
J=.089;
rr=.816;
t=0;
i=0;
dt=.0001;
P=4;
Tl=11.9/2;
Te=0;
tet0=0;tetr0=0;tet=0;tetr=0;
rs=.435;
Wr0=0;
Xlr=.754;
Xls=.754;
Wb=120*pi;
Xm=26.13;
Xss=Xls+Xm;
Xrr=Xlr+Xm;
D=(Xss*Xrr)-(Xm^2);
vqr=0;vdr=0;vor=0;
Q0=[0;0;0;0;0;0];
Qqs=0;Qds=0;Qos=0;Qqr=0;Qdr=0;Qor=0;
while t<=3
Vas=220*(.8165)*cos(Wb*t);
Vbs=220*(.8165)*cos((Wb*t)-(2*pi/3));
Vcs=220*(.8165)*cos((Wb*t)+(2*pi/3));
Ks=(2/3)*[cos(tet0) cos((tet0)-(2*pi/3)) cos((tet0)+(2*pi/3));sin(tet0) sin((tet0)-(2*pi/3)) sin((tet0)+(2*pi/3));.5 .5 .5];
V1=Ks*[Vas;Vbs;Vcs];
vqs=V1(1,1);vds=V1(2,1);vos=V1(3,1);
Q=[Qqs;Qds;Qos;Qqr;Qdr;Qor];
V=[vqs;vds;vos;vqr;vdr;vor];
Wr=Wr0;
W=Wr;
A=[rs*Xrr/D (W/Wb) 0 (-rs*Xm/D) 0 0;(-W/Wb) rs*Xrr/D 0 0 -rs*Xm/D 0;0 0 rs/Xls 0 0 0;-rr*Xm/D 0 0 rr*Xss/D (W-Wr)/Wb 0;0 (-rr*Xm/D) 0 (-(W-Wr)/Wb) rr*Xss/D 0;0 0 0 0 0 rr/Xlr];
B=[1/Wb 0 0 0 0 0;0 1/Wb 0 0 0 0;0 0 1/Wb 0 0 0;0 0 0 1/Wb 0 0;0 0 0 0 1/Wb 0;0 0 0 0 0 1/Wb];
Brev=inv(B);
Arev=-inv(B)*A;
Q01=Arev*Q+Brev*V;
Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))-(Q(2,1)*Q(4,1)));
Wr01=(P/2)*((Te-Tl)/J);
tet01=W;
tetr01=Wr;
Wr=Wr0+(Wr01*dt/2);
tet=tet0+(tet01*dt/2);
tetr=tetr0+(tetr01*dt/2);
Q=Q0+(Q01*dt/2);
Q02=Arev*Q+Brev*V;
Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))-(Q(2,1)*Q(4,1)));
Wr02=(P/2)*((Te-Tl)/J);
Wr=Wr0+(Wr02*dt/2);
W=Wr;
tet02=W;
tetr02=Wr;
tet=tet0+(tet02*dt/2);
tetr=tetr0+(tetr02*dt/2);
Q=Q0+(Q02*dt/2);
Q03=Arev*Q+Brev*V;
Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))-(Q(2,1)*Q(4,1)));
Wr03=(P/2)*((Te-Tl)/J);
Wr=Wr0+(Wr03*dt);
W=Wr;
tet03=W;
tetr03=Wr;
tet=tet0+(tet03*dt);
tetr=tetr0+(tetr03*dt);
Q=Q0+(Q03*dt);
Q04=Arev*Q+Brev*V;
Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))-(Q(2,1)*Q(4,1)));
Wr04=(P/2)*((Te-Tl)/J);
Wr0=Wr0+(Wr01+2*Wr02+2*Wr03+Wr04)*(dt/6);
W=Wr0;
tet04=W;
tetr04=Wr;
tet0=tet0+(tet01+2*tet02+2*tet03+tet04)*(dt/6);
tetr0=tetr0+(tetr01+2*tetr02+2*tetr03+tetr04)*(dt/6);
Q0=Q0+(Q01+Q02*2+2*Q03+Q04)*(dt/6);
Qqs=Q0(1,1);Qds=Q0(2,1);Q0s=Q0(3,1);Qqr=Q0(4,1);Qdr=Q0(5,1);Q0r=Q0(6,1);
Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))-(Q(2,1)*Q(4,1)));
I=(1/D)*[Xrr 0 0 -Xm 0 0;0 Xrr 0 0 -Xm 0;0 0 D/Xls 0 0 0;-Xm 0 0 Xss 0 0;0 -Xm 0 0 Xss 0;0 0 0 0 0 D/Xlr]*Q;
iqs=I(1,1);ids=I(2,1);ios=I(3,1);iqr=I(4,1);idr=I(5,1);ior=I(6,1);
Kr=(2/3)*[cos((tet0-tetr0)) cos(((tet0-tetr0))-(2*pi/3)) cos(((tet0-tetr0))+(2*pi/3));sin((tet0-tetr0)) sin(((tet0-tetr0))-(2*pi/3)) sin(((tet0-tetr0))+(2*pi/3));.5 .5 .5];
Irotor=inv(Kr)*[iqr;idr;ior];
iar=Irotor(1,1);ibr=Irotor(2,1);icr=Irotor(3,1);
Ks=(2/3)*[cos(tet0) cos((tet0)-(2*pi/3)) cos((tet0)+(2*pi/3));sin(tet0) sin((tet0)-(2*pi/3)) sin((tet0)+(2*pi/3));.5 .5 .5];
Istator=inv(Ks)*[iqs;ids;ios];
ias=Istator(1,1);ibs=Istator(2,1);ics=Istator(3,1);
i=i+1;
time(i)=t;
Iar(i)=iar;
Tee(i)=Te;
Ias(i)=ias;
WW(i)=(30*Wr0)/(2*pi);
t=t+.0001;
if t>=1.5
Tl=11.9;
end
end
plot(time,WW);xlabel(‘t’) ;ylabel(‘Wr’)
grid on
figure
plot(time,Ias);xlabel(‘t’) ;ylabel(‘ias’)
grid on
figure
plot(time,Iar);xlabel(‘t’) ;ylabel(‘iar’)
grid on
figure
plot(time,Tee);xlabel(‘t’) ;ylabel(‘Te’)
grid on
figure
plot(WW,Tee);xlabel(‘wr’) ;ylabel(‘Te’)
grid on
با توجه به متن برنامه متلب در ابتدا موتور را بی بار راه اندازی می کنیم و نتیجه ای که از خروجی متلب مشاهده می کنیم:
- انجام پروژه متلب با سایت متلبی
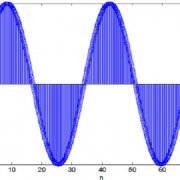
در این شکل می بینیم که سرعت گردش روتور از صفر تا 1800rpm افزایش می یابد و بعد ثابت می ماند, چون به سرعت نامی خود رسیده است. Wb

جریان استاتور با متلب
در شکل فوق جریان استاتور را در طول زمان اجرای برنامه متلب می بینیم.

جریان روتور با متلب
شکل بالا تغییرات جریان روتور را به نمایش گذاشته است
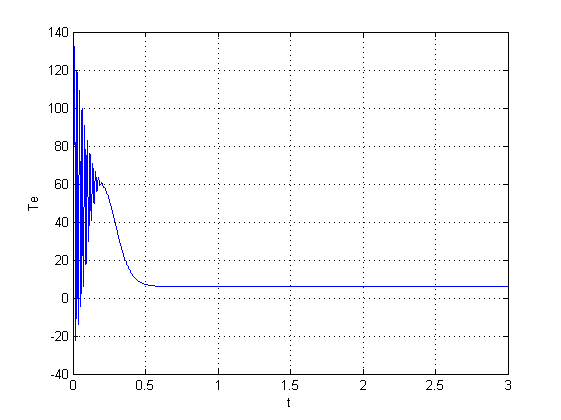
گشتاور موتور القایی با متلب
در شکل بالا گشتاور الکترومغناطیسی بعد از نوسانات ابتدایی به صفر می رسد, حالا اگر بخواهیم گشتاور را بر حسب سرعت در متلب داشته باشیم به صورت زیر به دست می آید:

بعد از بررسی ویژگی ماشین القایی مادامی که بی بار کار می کند میتواند بار نامی مکانیکی را روی محور ماشین القایی قرار داد. برای اینکار در برنامه متلب چند خط زیر را اضافه می کنیم:
if t>=1.5
Tl=11.9;
end
با اضافه کردن این قسمت از برنامه که در بالا با رنگ سبز نیز مشخص شده, این اتفاق در متلب می افتد و نتایج به صورت زیر است:
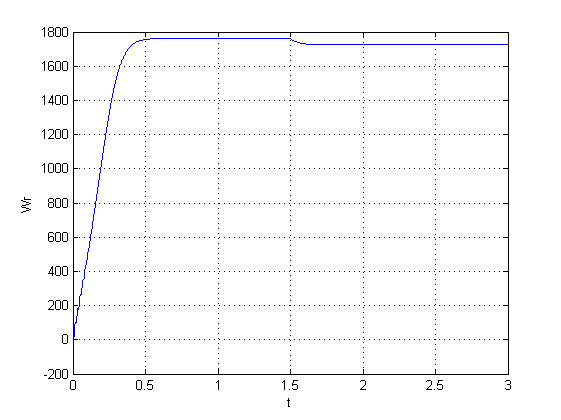
راه اندازی موتور القایی با متلب
همانطور که از شکل فوق مشخص هست در حالتی که بار روی محور ماشین القایی قرار می گیرد سرعت 1800rpm نمی شود و کمی افت دارد.
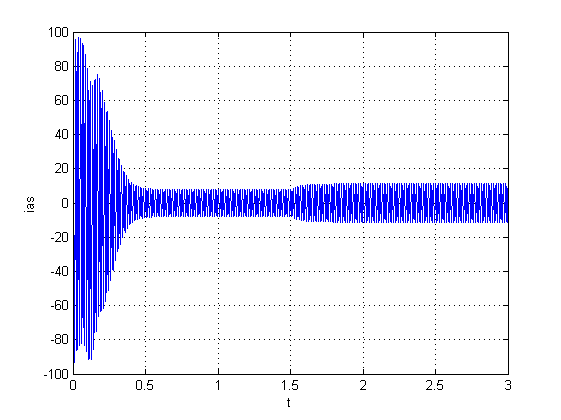
جریان استاتور با متلب
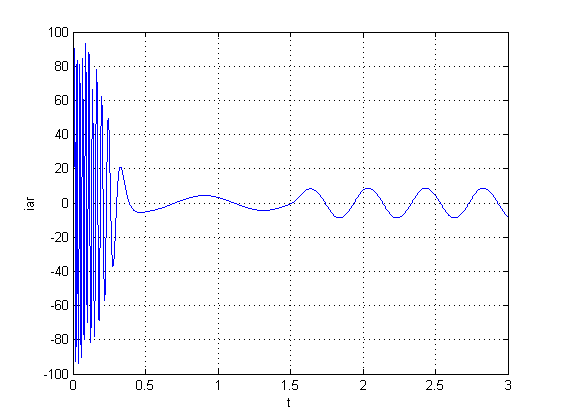
جریان روتور با متلب
دلیل نوسانات در جریان روتور و استاتور قرار گرفتن بار نامی روی محور ماشین است
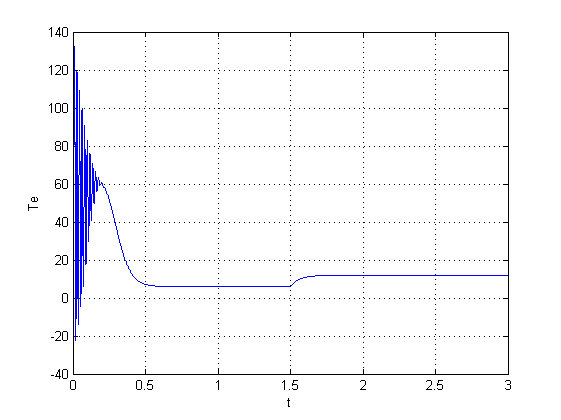
همانطور که مشاهده می شود گشتاور مغناطیسی در یک مقدار غیر از صفر ثابت می ماند.

بزودی بخش دیگری از تحلیل رفتار موتور القایی را در متلب در سایت متلبی خواهید دید.