پیش بینی قیمت دلار و طلا با شبکه عصبی و الگوریتم ژنتیک در متلب

قصد داریم در این پست آموزش متلب, پیش بینی قیمت دلار و طلا را به روش های الگوریتم ژنتیک و شبکه عصبی LMP و RBF و LMS و BP انجام دهیم
دیتا را از سایتهای معتبر جهانی گرد آوری کردیم و در قالب یک فایل اکسل در آوردیم.
فایل های پروژه آماده متلب در پایان همین پست قرار گرفته است
مشخصات دیتا:
این دیتاست دو ورودی و یک خروجی دارد و برای ارزیابی دقت پیش بینی از 5 روش متداول در آنالیز شبکه های عصبی استفاده شده است و به منظور وزندهی بهتر نرونهای عصبی ابتدا نرمالیزاسیون بین صفر تا یک و سپس تقسیم دیتا به دسته آموزش و تست به نسبت 70 به 30 صورت گرفته است.

و در هر روش ابتدا ساختار اولیه شبکه عصبی مورد نظر ساخته شده و سپس دستور آمورش صادر شده و سپس دقت آموزش را برای داده آموزش و تست محاسبه کرده و این روال برای هر 5 روش در این پروژه متلب استفاده شده است.

clc;close all;rng(‘default’)

warning off ;

global Xtrain Ytrain net Xtest Ytest

متغیر گلد با پسوند مت فراخوانی میشود

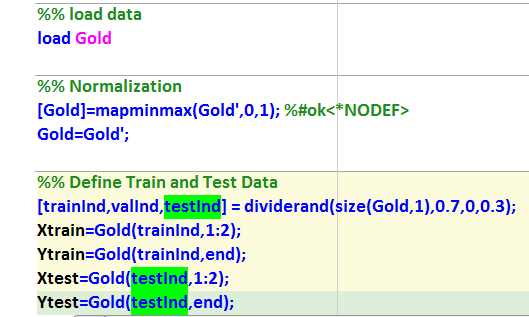
%% load data

load Gold

نرمالیزاسیون دیتا

%% Normalization

[Gold]=mapminmax(Gold’,0,1); %#ok<*NODEF>

Gold=Gold’;

%% Define Train and Test Data

[trainInd,valInd,testInd] = dividerand(size(Gold,1),0.7,0,0.3);

Xtrain=Gold(trainInd,1:2);

Ytrain=Gold(trainInd,end);

Xtest=Gold(testInd,1:2);

Ytest=Gold(testInd,end);

شبکه پرسپترون چندلایه

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% MLP

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

fprintf(‘\n———-MLP————————\n’)

% Set up network parameters.

nin = 2; % Number of inputs.

nhidden = 3; % Number of hidden units.

nout = 1; % Number of outputs.

alpha = 0.01; % Coefficient of weight-decay prior.

% Create and initialize network weight vector.

net = mlp(nin, nhidden, nout, ‘linear’, alpha);

% Train using scaled conjugate gradients.

options = zeros(1,18);

options(1) = 0; % This provides display of error values.

options(14) = 100; % Number of training cycles.

[net, options] = netopt(net, options, Xtrain, Ytrain, ‘scg’);

y1 = mlpfwd(net, Xtrain);

y2 = mlpfwd(net, Xtest);

train_Error=(sum(Ytrain-y1).^2)/length(Ytrain)

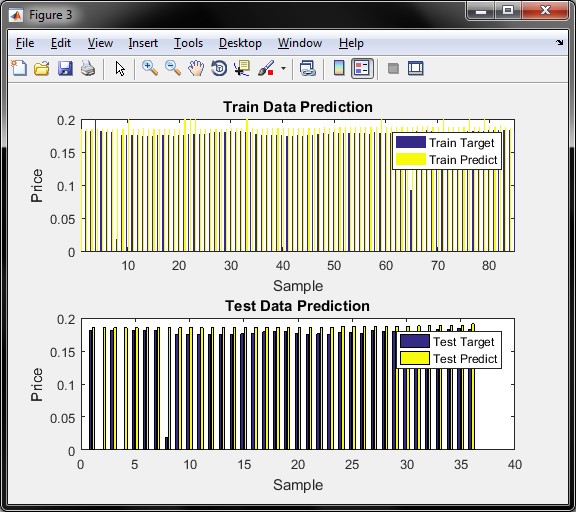
figure

subplot(211)

bar([Ytrain y1])

legend(‘Train Target’,’Train Predict’)

title(‘Train Data Prediction’)

set(gca,’xlim’,[1 numel(y1)],’ylim’,[0 0.2])

ylabel(‘Price’)

xlabel(‘Sample’)

subplot(212)

bar([Ytest y2])

title(‘Test Data Prediction’)

legend(‘Test Target’,’Test Predict’)

ylabel(‘Price’)

xlabel(‘Sample’)

test_Error=(sum(Ytest-y2).^2)/length(Ytest)

شبکه عصبی شعاعی با تابع گوسی

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% RBF

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

fprintf(‘\n—————RBF——————-\n’)

% Create and initialize network weight and parameter vectors.

Net = rbf(nin, nhidden, nout, ‘gaussian’);

net = rbftrain(net, options, Xtrain, Ytrain);

[y3, act2] = rbffwd(net, Xtrain);

[y4, act2] = rbffwd(net, Xtest);

figure

subplot(211)

bar([Ytrain y3])

legend(‘Train Target’,’Train Predict’)

title(‘Train Data Prediction’)

set(gca,’xlim’,[1 numel(y3)],’ylim’,[0 0.2])

ylabel(‘Price’)

xlabel(‘Sample’)

subplot(212)

bar([Ytest y4])

title(‘Test Data Prediction’)

legend(‘Test Target’,’Test Predict’)

ylabel(‘Price’)

xlabel(‘Sample’)

train_Error=(sum(Ytrain-y3).^2)/length(Ytrain)

test_Error=(sum(Ytest-y4).^2)/length(Ytest)

شبکه عصبی با حداقل مربعات

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% LMS

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

fprintf(‘\n———-LMS————————\n’)

%% Train least square Neural Network

[w1,y5,f]=mlplms(Xtrain’,Ytrain,1e-2,100);

%% Predicion Result

figure

subplot(211)

bar([Ytrain y5′])

legend(‘Train Target’,’Train Predict’)

title(‘Train Data Prediction’)

set(gca,’xlim’,[1 numel(y5)],’ylim’,[0 0.2])

ylabel(‘Price’)

xlabel(‘Sample’)

train_Error=(sum(Ytrain-y5′).^2)/length(Ytrain)

%% Test Result

Xtestc=[ones(1,size(Xtest’,2));Xtest’];

y6=double(f(w1’*Xtestc));

test_Error=(sum(Ytest-y6′).^2)/length(Ytest)

subplot(212)

bar([Ytest y6′])

title(‘Test Data Prediction’)

legend(‘Test Target’,’Test Predict’)

ylabel(‘Price’)

xlabel(‘Sample’)

شبکه عصبی بازگشتی لونبرگ

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% BP

% (levenberg)

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

fprintf(‘\n————-BP———————\n’)

% Create a Fitting Network

hiddenLayerSize = 4;

trainFcn = ‘trainlm’; % Levenberg-Marquardt backpropagation.

net = fitnet(hiddenLayerSize,trainFcn);

net.plotFcns = {‘plotperform’};

% Train the Network

[net,tr] = train(net,Xtrain’,Ytrain’);

% Test the Network

y7 = net(Xtrain’);

y8 = net(Xtest’);

%% Test Result

train_Error=(sum(Ytrain-y7′).^2)/length(Ytrain)

test_Error=(sum(Ytest-y8′).^2)/length(Ytest)

%% Predicion Result

figure

subplot(211)

bar([Ytrain y7′])

legend(‘Train Target’,’Train Predict’)

title(‘Train Data Prediction’)

set(gca,’xlim’,[1 numel(y7)],’ylim’,[0 0.2])

ylabel(‘Price’)

xlabel(‘Sample’)

subplot(212)

bar([Ytest y8′])

title(‘Test Data Prediction’)

legend(‘Test Target’,’Test Predict’)

ylabel(‘Price’)

xlabel(‘Sample’)

شبکه بازگشتی با آموزش ژنتیک به منظور تعیین ضرایب بهینه وزن نرونها

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% BP+GA

% (Genetic)

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

fprintf(‘\n—————BPGA——————-\n’)

net = fitnet(hiddenLayerSize,trainFcn);

net.trainParam.showWindow=0;

% Train the Network

[net,tr] = train(net,Xtrain’,Ytrain’);

opts = gaoptimset(…

‘PopulationSize’, 50, …

‘Generations’, 100, …

‘PlotFcns’,{ @gaplotbestf,@gaplotbestindiv});

ub=[2*ones(1,1+hiddenLayerSize^2)];

lb=-ub;

[xbest] = ga(@costga, numel(lb), [], [], [], [], …

lb, ub, [], [], opts);

net=setwb(net,xbest);

% Test the Network

y9 = net(Xtrain’);

y10 = net(Xtest’);

%% Test Result

train_Error=(sum(Ytrain-y9′).^2)/length(Ytrain)

test_Error=(sum(Ytest-y10′).^2)/length(Ytest)

%% Predicion Result

figure

subplot(211)

bar([Ytrain y9′])

legend(‘Train Target’,’Train Predict’)

title(‘Train Data Prediction’)

set(gca,’xlim’,[1 numel(y9)],’ylim’,[0 0.2])

ylabel(‘Price’)

xlabel(‘Sample’)

subplot(212)

bar([Ytest y10′])

title(‘Test Data Prediction’)

legend(‘Test Target’,’Test Predict’)

ylabel(‘Price’)

xlabel(‘Sample’)

fprintf(‘\n———————————-\n’)

تابع هدف بهینه سازی ژنتیک با نام costga در جهت کاهش خطای داده اموزش و تست عمل میکند و متغیرهای خزوجی داده اموزش و تست در متغیر y1 تا y10 بترتیب ظاهر میگردد که در حافظه ورک اسپس متلب قابل رویت است و نتایج خطای روشهای پیشنهادی بصورت زیر است
خطای اموزش و خطای تست برای هر روش با اجرای برنامه متلب mainGold قابل رویت است:

———-MLP————————

Warning: Maximum number of iterations has been exceeded

train_Error =

3.8330e-08

test_Error =

0.0161

—————RBF——————-

Warning: Maximum number of iterations has been exceeded

train_Error =

1.7120e-27

test_Error =

0.0164

———-LMS————————

train_Error =

0.0107

test_Error =

0.0177

————-BP———————

train_Error =

0.0043

test_Error =

0.0309

—————BPGA——————-

Optimization terminated: average change in the fitness value less than options.FunctionTolerance.

train_Error =

5.8291e-04

test_Error =

0.0014

———————————- >>

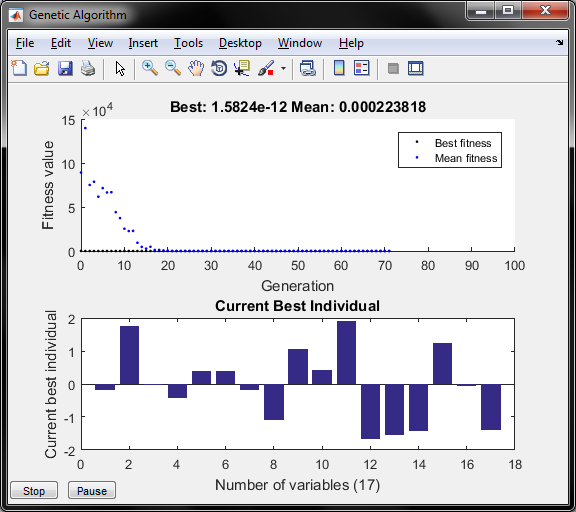
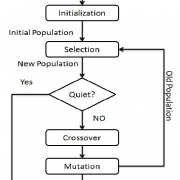
که نمودار همگرای ژنتیک در رسیدن به خطای پیش بینی کمتر بصورت زیر است:

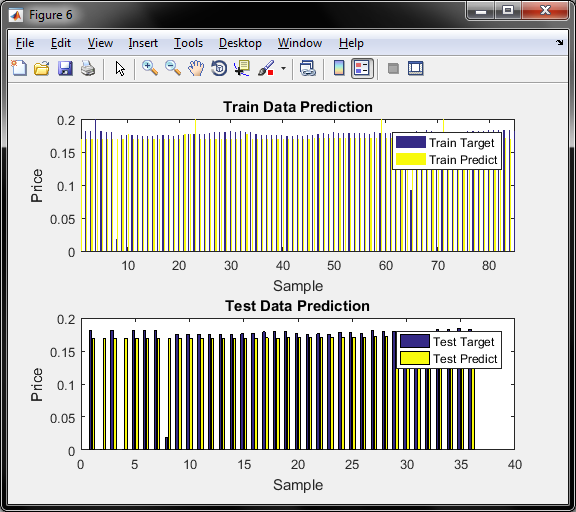
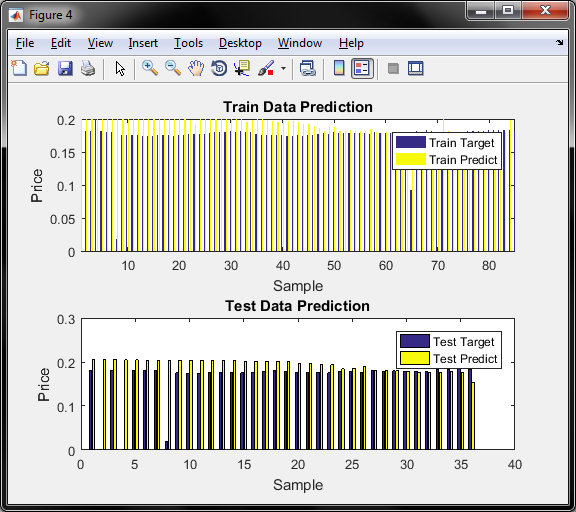
و نمودار میله ای در شکل مقدار وزن نرونهای شبکه لایه پنهان و خروجی ( مجموع 17 وزن ) را نشان میدهد و در مجموع روش ژنتیک بدلیل بهینه سازی وزن نرونها در مجموع داده آموزش و تست دارای خطای کمتری است و نمودار مقایسه داده های اموزش و تست هر روش جداگانه رسم می شود و برای مثال در روش ژنتیک بصورت زیر ظاهر می شود.

این پروژه در متلب 2016 تست و اجرا شده است.
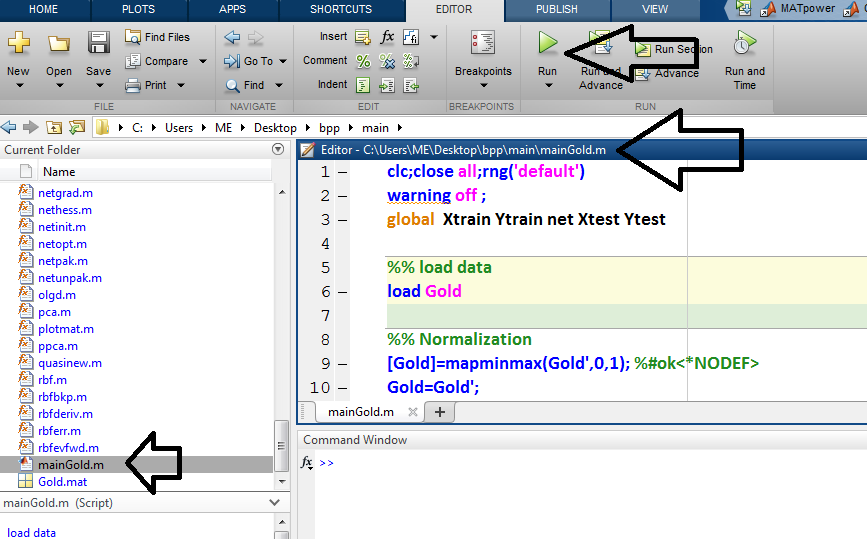
لازم بذکر است که فقط و فقط فایل اصلی پروژه با نام mainGold باید فراخوانی و اجرا گردد و فایلهای دیگر فانکشن هستند که در طول اجرای شبیه سازی توسط برنامه اصلی فراخوانی میشود و به هیچ وجه این فانکشن ها قابلیت اجرا ندارند.
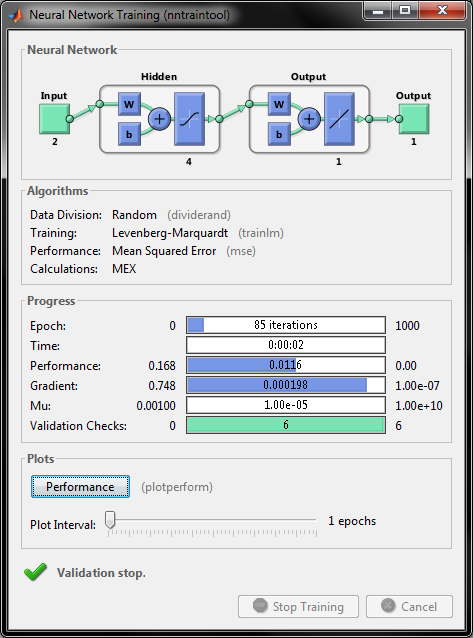
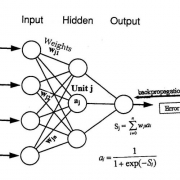
شکل زیر مربوط به اجرای فایل چندلایه بازگشتی است که در قسمت بالایی ان نشان میدهد که سیستم عصبی دارای دو ورودی و 4 نرون در لایه پنهان و نهایتا یک خروجی است و روش اموزش روش لونبرگ است.

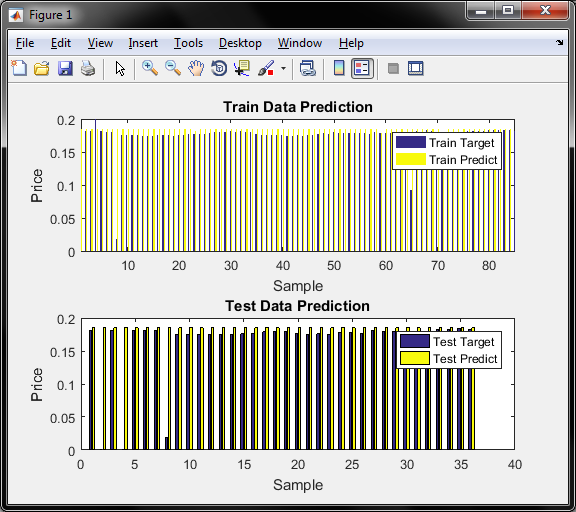
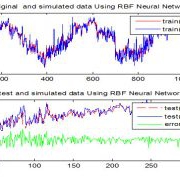
و با اجرای برنامه 5 نمودار بدست می آید که نمودار یک دقت قیمت برای داده اموزش و تست برای روش MLP را نشان میدهد

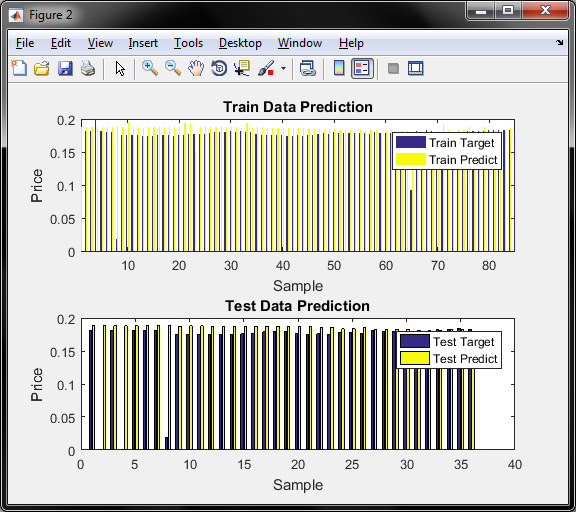
نمودار دو دقت قیمت برای داده اموزش و تست برای روش RBF را نشان میدهد

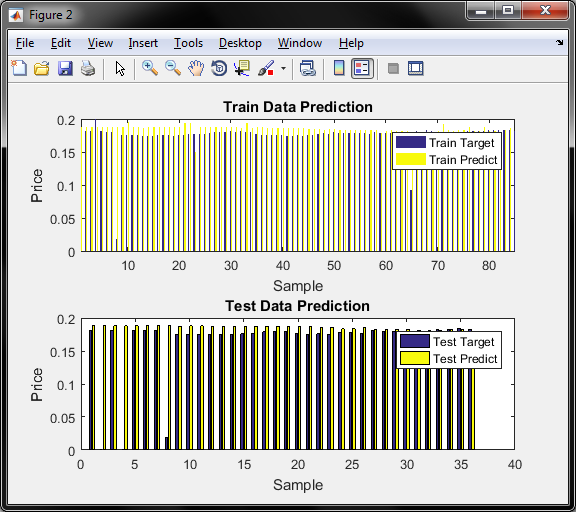
نمودار سوم دقت قیمت برای داده اموزش و تست برای روش LMS را نشان میدهد

نمودار چهارم دقت قیمت برای داده اموزش و تست برای روش BP را نشان میدهد

نمودار پنچم دقت قیمت برای داده اموزش و تست برای روش GA را نشان میدهد

نحوه اجرای برنامه متلب بصورت زیر است

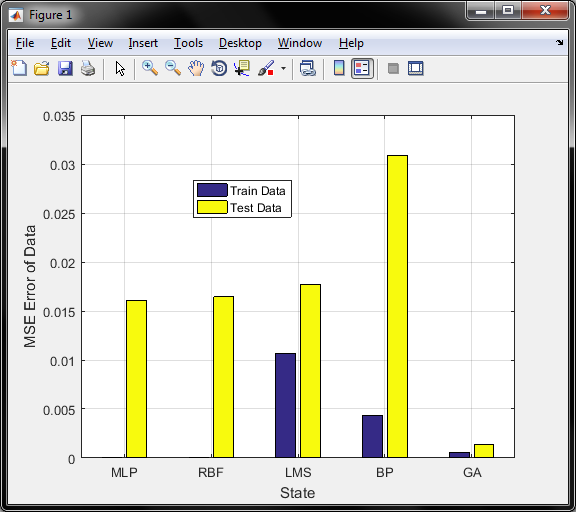
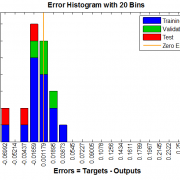
نتایج نمودار میله ای خطای روشها برای داده تست و اموزش بصورت زیر می شود که برای دو روش اول چون خطای آموزش بسیار بسیار کم بوده در نمودار قابل رویت نیست و در مجموع خطای داده تست و اموزش , روش ژنتیک بهترین بوده

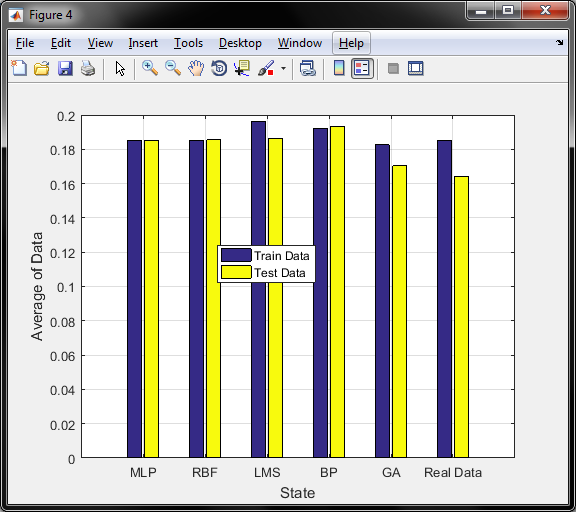
و همچنین نمودار متوسط مقدار روشها در مقایسه با میانگین قیمت طلای داده تست و اموزش بصورت زیر است

و طبق شکل فوق , روش ژنتیک کمترین اختلاف را با داده واقعی برای داده تست و آموزش دارد
و در مورد معیار سنجش محور عمودی , همان قیمت طلای 18 عیار است که با توجه به دیتای موجود و نزدیکی قیمتها به یکدیگر و بمنظور پیش بینی دقیق تر , قیمتها را بر عددی بزرگ مثلا در اینجا 700 هزار تقسیم کرده و بدین صورت نرمالیزه شده و اعداد بین 0.15 تا 0.2 نرمالیزه میگردد