پروژه شناسایی سیستم با متلب
پروژه شناسایی سیستم
فصل اول: معرفی سیستم ، خطی سازی و نمایش حالت های مختلف سیستم جهت شناسایی سیستم با متلب
معرفی سیستم و معادلات حاکم برآن:
Cart_pendulum system ، سیستمی مکانیکی میباشد بدین صورت که مرکزیت جرم سیستم در بالای محور به تعادل رسیده است. نمونه ای از Cart_pendulum system در شکل زیر به نمایش گذاشته شده است.
معادلات این سیستم در حالت کلی همچون سیستم جرم و فنر میباشد و دینامیک سیستم در حالت کلی به صورت زیر میباشد.
که در اینجا M(q) ماتریس Inertia، C(q,q’) نشان دهنده نیروهای کوریلیس، K(q) نیروی مربوط به انرژی پتانسیل و B(q) نیز مربوط به نحوه تاثیر نیروهای خارجی بر روی سیستم است.
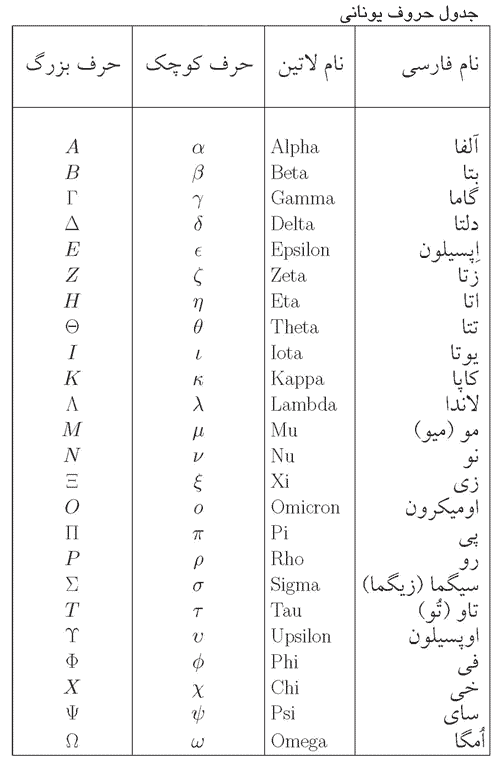
برای مدل سازی این سیستم متغیرهای حالت را موقعیت و سرعت انتخاب میکنیم. و از نماد رو و روآلفا و برای آن استفاده میکنیم. برای نمایش زاویه و سرعت زاویه ای نیز از نماد تتا و تتاآلفا استفاده میکنیم.
در این سیستم باید با توجه به حرکت کارت ،پاندول به صورت عمودی موقعیت خود را حفظ کند.
F نیرویی است که به صورت افقی وارد میشود.
با این تفاسیر معادلات دینامیکی سیستم به صورت زیر بدست میآید.
M جرم سطح میباشد. m و J جرم و ممان اینرسی سیستمی که قراره کنترل شود هستند. فاصله بین سطح تا مرکز جرم سیستم میباشد.
برای بازنویسی معادلات در فضای حالت از متغیرهای زیر استفاده میکنیم.
در اینجا چون به یک سیستم تک ورودی تک خروجی نیاز داریم خروجی را برابر زاویه در نظر می گیریم.
شناسایی سیستم با متلب- خطی سازی سیستم:
برای خطی سازی سیستم فوق حول نقطه صفر(نگه داشتن پاندول بصورت عمودی) از دو تقریب زیر استفاده می کنیم.
توجه به کوچک بودن زاویه میتوان سینوس را معادل θ و کسینوس را معادل 1 در نظر گرفت. همچنین از آنجایی که مشتق θبسیار کوچک است میتوان از مرتبه 2 آن صرف نظر کرد.بنابراین به سیستم زیر خواهیم رسید.
با جایگذاری مقادیر به ماتریس های زیر میرسیم.
Mt=M+m
Jt=J+m*l^2
µ=Mt*Jt – m^2*l^2
M=0.5kg
m=0.5kg
C=0.1 N/m.sec friction of the cart
L=0.3m
J=0.006Kg*m^2 inertia of the pendulum
g=9.8
با جایگذاری مقادیر بالا ، ماتریس های حالت سیستم خطی شده بصورت زیر در می آید:
A=
0 0 1.0000 0
0 0 0 1.0000
0 7.7368 -0.1789 0
0 51.5789 -0.5263 0
B=
0
0
1.7895
5.2632
C=
0 1 0 0
D=
0
که با استفاده از دستور ss2tf(A,B,C,D) می توان تابع تبدیل سیستم خطی شده را بدست آورد که بصورت زیر می باشد
شبیه سازی سیستم خطی شده و کنترل شده :
تابع تبدیل سیستم خطی به صورت زیر است:
همانطور که از مخرج تابع تبدیل پیداست سیستم فوق ناپایدار میباشد.با روش LQR سیستم فوق را میتوان پایدار نمود.
دستورات این سیستم در زیر آورده شده است .ابتدا ماتریس Q به صورت مقابل تعریف میشود.
>> Q=C’*C
Q =
1 0 0 0
0 1 0 0
0 0 0 0
0 0 0 0
خال با استفاده از دستورlqr ،گین فیدبک محاسبه میگردد.
>> k=lqr(ss(A,B,C,D),Q,1)
k =
-1.0000 24.0733 -1.8097 3.5846
ماتریس جدید A با عنوان An به صورت مقابل تعریف میگردد. از این پس از این ماتریس در محاسبات استفاده میکنیم
>> An=A-B*k
An =
0 0 1.0000 0
0 0 0 1.0000
1.7895 -35.3417 3.0594 -6.4145
5.2632 -75.1225 8.9982 -18.8662
اکنون تابع تبدیل حلقه باز سیستم کنترل شده به صورت زیر میباشد و از این به بعد با این سیستم پایدار کار می کنیم.
تابع تبدیل سیستم خطی شده و کنترل شده را بصورت زیر در متلب شبیه سازی می کنیم:
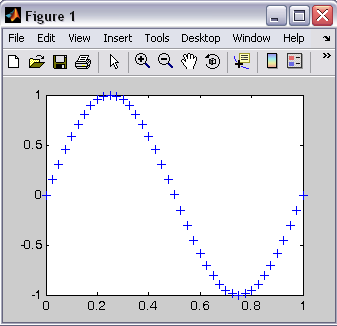
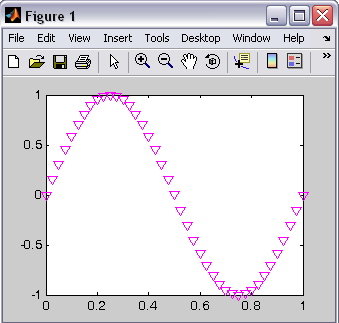
پاسخ پله سیستم خطی شبیه سازی شده بصورت زیر می باشد:
همچنین در ادامه سیستم غیر خطی را در سیمولینک بصورت زیر شبیه سازی می کنیم:
پاسخ سیستم غیر خطی دارای نوسان میباشد که حل این مشکل از کنترل کننده PID استفاده شده است. پارامترهای کنترلر PID به شرح مقابل است.
Kp=40 Ki=10 Kd=2
پاسخ پله سیستم غیر خطی نیز در زیر آورده شده است:
همانگونه که در شکل زیر می بینیم رفتار سیستم خطی و غیز خطی تفاوت چندانی باهم ندارند و مشابه یکدیگرند.
همپنین فایل شبیه سازی تمام موارد در پوشه ای جداگانه ضمیمه گزارش شده است.
1- شناسایی سیستم با متلب, حالات مختلف نمایش پیوسته سیستم:
1-1) معادلات حالت پیوسته
می توان رابطه بین ورودی و خروجی را به فرم معادلات فضاي حالت به صورت زير نشان داد که حالت سیستم و خروجی و ورودی هستند. ماتریس های حالت سیستم ما در زیر آورده شده است.
A =
0 0 1.0000 0
0 0 0 1.0000
1.7895 -35.3417 3.0594 -6.4145
5.2632 -75.1225 8.9982 -18.8662
B=
0 0 1.7895 5.2632
C=
0 1 0 0
D= 0
با توجه به اینکه در ایجا فقط خروجی زاویه را مد نظر داریم از این پس با ماتریس های بالا کار می کنیم.
1-2) تابع تبديل پيوسته
با استفاده از دستور زیر تابع تبديل سیستم را بدست مي آوريم
[num,den]=ss2tf(A,B,C,D)
sys=tf(num,den)
1-3)معادلات ديفرانسيل خطي همگن با ضرايب ثابت
از روي تابع تبديل معادله ديفرانسيل خطي بدست مي آيد. که در حقیقت یک رابطه مشتقی انتگرالی بین عناصر است.
1-4)پاسخ ضربه پیوسته
به کمک دستور ilaplace در متلب میتوان پاسخ ضربه سیستم را بدست آورد.
gn=ilaplace(5.26*s^2)/(s^4+15.8068*s^3+73.3318*s^2+88.1821*s+51.5789)
پاسخ سیستم به ورودی ضربه
1-5)پاسخ فرکانسی سیستم
در این بخش نیز پاسخ سیستم را به کمک نرم افزار متلب بدست می آوریم.
Bod(sys)
تابع تبدیل در حوزه فرکانس
2- حالات مختلف نمایش سیستم در حالت گسسته:
2-1)فضای حالت سیستم بصورت گسسته:
(F,G,C,D)=ssdata(sys10)
F =
-15.8068 -9.1666 -2.7557 -1.6118
8.0000 0 0 0
0 4.0000 0 0
0 0 1.0000 0
G =
1 0 0 0
C =
0 0.6579 0 0
D = 0
2-2)تابع تبدیل سستم در حالت گسسته
Gz=c2d(sys,.1)
Transfer function:
0.01567*z^3 – 0.02209*z^2 – 0.00283*z + 0.009249
————————————————
z^4 – 2.832 z^3 + 2.914 z^2 – 1.285 z + 0.2058
Sampling time: 0.1
2-3)معادلات تفاضلی سیستم
0.01567u(k+3) – 0.02209u(k+2) – 0.00283u(k+1) + 0.009249u(k)=
y(k+4) – 2.832y(k+3) + 2.914u(k+2) – 1.285u(k+1) + 0.2058u(k)
2-4)پاسخ ضربه سیستم گسسته
gz=iztrans((.01567*z^3 -.02209*z^2 -.00283*z +.009249)/(z^4 – 2.832*z^3 + 2.914*z^2 -1.285*z +.2058))
2-5)پاسخ فركانسي گسسته
براي بدست آوردن پاسخ فركانسي گسسته كافيست در تابع تبديل گسسته به جاي z ، قرار مي دهيم:
تابع تبدیل گسسته سیستم در حوزه فرکانس:

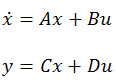

دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.