راهکار ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
ترجمه مقاله:
A Q-Learning Based Adaptive Bidding Strategy in Combinatorial Auctions
راهکار ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
چکیده
در سالهای اخیر، حراجهای ترکیبی، که در آن پیشنهاددهندگان اجازه دارند پیشنهادات خویش را در مورد دسته ای از اقلام ارائه کنند، مورد تحقیق بسیاری قرار گرفته اند.
حراجهای ترکیبی هنگامی که پیشنهاددهندگان دارای اقلام مکمل و قابل جایگزینی دارند، می توانندبه کارایی های بهتر اجتماعی دست یابند. با اینکه بسیاری از کارها بر روی حراجهای ترکیبی صورت گرفته است، بسیاری از آنها بر مسئله تعیین برنده و طرح حراج متمرکز هستند.
بخش عمده پژوهش نشده در زمینه حراجههای ترکیبی راهکارهای ارائه پیشنهاد است. ما در این مقاله، یک راهکار ارائه پیشنهاد تطبیقی مبتنی بر Q- یادگیری برای حراجهای ترکیبی در این بازارهای ایستا پیشنهاد می کنیم.
پیشنهاد دهنده با بکارگیری این راهکار می تواند از وضعیت های مختلف عبور کرده و به تدریج با وضعیت مطلوب همگرایی نموده و منفعت زیادی را در دراز مدت کسب کند.
نتایج آزمایشی نشان می دهند که راهکار تطبیقی مبتنی بر Q- یادگیری در مقایسه با راهکار مطلوب نسبتا خوب عمل کرده و راهکار تصادفی و راهکار تطبیقی قبلی ما را در محیط های مختلف بازار، حتی بدون هیچ دانش قبلی، اجرا می کند.
کلیدواژه ها: راهکار ارائه پیشنهاد، تطبیقی، Q- یادگیری، حراجهای ترکیبی
- مقدمه
در سالهای اخیر، با افزایش تقاضای منابع محاسباتی برای مسائل محاسباتی علمی پیچیده، مثل محاسبه نجومی و محاسبه بیولوژیکی، سودمندی قدرت محاسبه که با زیرساخاتهای توزیعی و متمرکز فراهم شده، از سوی دانشمندان و محققان علم کامپیوتر مورد توجه بیش از پیش قرار گرفته است.
اینترنت نمونه ای موردی از زیرساخت مذکور است که کاربران متفاوتی در آن می توانند از منابع محاسباتی فراهم شده برای انجام وظایف خویش بهره بگیرند. این نوع مسئله تخصیص منبع، یعنی نحوه تخصیص این منابع در بین گروهی از کاربران، تبدیل به موضوع مهمی شده است.
در مقایسه با سایر روشهای تخصیص منبع، حراج اینترنتی مزیت عمده ای دارد که منابع را به پیشنهاددهندگانی اختصاص می دهد که به آنها ارزش بسیار زیادی قائل شده و از نظر علم اقتصاد تخصیص کافی را بدست می آورند.
در بین تمامی انواع حراج، حراجهای ترکیبی، که پیشنهاد دهندگان می توانند در مورد ترکیب اقلام پیشنهاد دهند، یعنی “بسته بندیها”، تا اقلام جداگانه، از سوی محققان در حوزه علوم کامپیوتر و اقتصاد مورد توجه بسیاری قرار گرفته است.
حراجهای ترکیبی هنگامی که پیشنهاد دهندگان دارای اقلام مکمل و قابل جایگزین بین کالاها باشند، می توانند به تخصیص های بیشتر اقتصادی منابع دست یابند تا حراجهای سنتی یک – قلم کالا.
این میزان تاکید کنندگی باعث افزایش کارایی می گردد که در بسیاری از کاربردها به اثبات رسیده است.
در دهه گذشته، کارهای زیادی در زمینه حراجهای ترکیبی انجام شده است.
دو مسئله ای که بیش از همه در سطح گسترده انجام گرفته است، تعیین برنده و طرح حراج است. مسئله تعیین برنده برای محاسبه تخصیص منابع در بین پیشنهاددهندگان است و اثبات شده است که دارای NP- مشکل می باشد.
برای حل این مسئله کارهای بسیاری اعم از یافتن راه حلهای مطلوب و راه حلهای تقریبی انجام شده است.
طرح حراج شامل طراحی پروتکلهای مختلف برای حراجهای ترکیبی مثل تک – دور در مقابل چند – دور، پیشنهاد- مهر و موم شده در مقابل پیشنهاد باز و اثبات- نام – غلط می باشد.
به علاوه، طرح مکانیسم محاسباتی برای حراجهای ترکیبی که برای طراحی محاسباتی ممکن است ضمن مکانیسم موثری برای حراجهای ترکیبی، حوزه پژوهشی در حال تغییری می باشد.
حوزه دیگر پژوهش در زمینه حراجهای ترکیبی طرح راهکارهای ارائه پیشنهاد می باشد.
همانطور که حراجهای ترکیبی در بسیاری از کاربردهای پروتکل حراج پیشنهاد- مهرو موم شده قیمت- اول تلفیق می شوند، ما توجه ویژه ای به راهکارهای ارائه پیشنهاد در این نوع حراج داریم.
برخلاف حراج ویکری، که ارائه پیشنهاد مفید راهکار غالبی می باشد، هیچ راهکار غالب و برجسته ای در حراجهای ترکیبی پیشنهاد- مهر و موم شده قیمت اول وجود ندارد که طرح راهکارهای ارائه پیشنهاد را به یک مسئله غیرمهم تبدیل کند.
با اینکه کارهای قبلی بر این مسئله تاکید دارند، راهکارهای پیشنهادی تطبیقی نیستند، به این معنا که نتایج بر اساس تحلیل بعدی ایجاد شده و به شرایط خاص بسیار محدود می باشند.
بر اساس اصول یادگیری- Q، ما در این مقاله یک راهکار ارائه پیشنهاد تطبیقی مبتنی بر یادگیری- Q پیشنهاد می کنیم.
پیشنهاد کننده با اتخاذ این راهکار می تواند از بین وضعیت های مختلف بر اساس سابقه ارائه پیشنهاد عبور کرده و در نتیجه نسبت به بازار پاسخ دهنده باشد.
پیشنهاد دهنده نیازی به دانش قبلی در مورد بازارها نداشته و بازارها به انواع معینی محدود می گردند.
به عبارتی دیگر، راهکار ما به خوبی تعمیم می یابد. به علاوه، راهکار تطبیقی پیشنهادی بر اساس یادگیری- Q به حراجهای ترکیبی محدود نمی شود.
در واقع، چنین راهکاری می تواند در هر حراج تکراری به کار رود، که در بخش نتیجه گیری مورد بحث بیشتری قرار خواهد گرفت.
ما توسط شبیه سازی ها نشان می دهیم که راهکار تطبیقی مبتنی بر یادگیری – Q به خوبی عمل می کند و در بازارهای مختلف در مقایسه با راهکار تصادفی و راهکار تطبیقی قبلی ما سودمندی های بسیاری ایجاد می کند.
همچنین عملکرد های راهکار ارائه پیشنهاد تطبیقی مبتنی بر یادگیری – Q و راهکار تطبیقی قبلی را به تفصیل مقایسه می کنیم.
به علاوه، می دانیم که پیشنهاد دهنده با استفاده ا زاین راهکار میتواند به سرعت با وضعیت بهینه در بازارهای مختلف همگرایی نموده و در نتیجه قادر به یادگیری و تطبیق، حتی بدون هیچ دانش قبلی می باشد.
- کارهای مربوطه
در حراجهای ترکیبی پیشنهاد- مهر و موم شده قیمت – اول، یک پیشنهاد دهنده دسته های متعدد نمایی را برای ارائه پیشنهاد در اختیار دارد.
مسئله تصمیم گیری که دسته ها انتخاب می کنند و میزان پیشنهادی که برای آنها ارائه می کنند، به ترتیب، راهکار دسته و راهکار قیمت نامیده می شوند.
در این بخش ما یک بررسی در زمینه هر دو راهکار در حراجهای ترکیبی ارائه می کنیم.
کار برهالت و همکاران، بر راهکار دسته در حراجهای ترکیبی یک – دور متمرکز می باشد.
آنها از حراجهای ترکیبی برای تخصیص حوزه های تحقیق نشده برای ربات های توزیع شده در یک حوزه بزرگ و پیشنهاد چهار راهکار ارائه پیشنهاد استفاده می کنند: سه – ترکیب، ترکیب – هوشمند، Greedy (آزمند) و Graph-Cut (برش- نمودار).
آنها با انجام آزمایشات نشان می دهند که حراجهای ترکیبی نسبت به حراجهای یک – قلم کالا به کارایی های بهتری دست می یابند و نتایج خوبی را در مقایسه با تخصیص های متمرکز شده مطلوب ایجاد می کنند.
همچنین تاثیرات راهکارهای متمرکز شده مطلوب را در مورد عملکردهای تیمی نشان می دهند، به صورتی که راهکار Graph-Cut به روشنی سه راهکار دیگر را اجرا می کند.
آنها دو راهکار دسته ای پیشنهاد می کنند: اینترنتی و رقابتی. پیشنهاد دهندگان با استفاده از راهکار اول در مورد دسته هایی پیشنهاد می دهند که بخاطر آن دارای ارزش گذاری های بیشتری باشند، ضمن اینکه پیشنهاددهندگان با استفاده از راهکار دوم در مورد دسته هایی پیشنهاد می دهند که برای آن دارای نسبت های بالاتری از ارزش گذاری بر اساس رقبای خویش برای برآوردهای قبلی شان باشد.
نتایج شبیه سازی نشان می دهند که پیشنهاددهندگان عاقل با استفاده از این دو راهکار نسبت به پیشنهاد دهندگان ساده که فقط پیشنهادات یک قلم کالا را می پذیرند، بهتر عمل می کنند.
آنها نیز تاثیر این دو راهکار را بر درآمدهای حراج گذار در حراجهای ترکیبی تحلیل می کنند.
Schwind و همکاران در تلاش برای حل مسئله تخصیص منابع محاسباتی با حراجهای ترکیبی چند- دور می باشند.
آنها وضعیتی را بررسی می کنند که در آن پیشنهاددهندگان از پول های رایج مجازی استفاده می کنند که با منابع بیهوده فروش بدست آمده اند و برای انجام وظایف خویش به منابع محاسباتی مورد نیاز دست می یابند.
آنها راهکارهای قیمت را برای دو نوع پیشنهاد کننده پیشنهاد می کنند:
پیشنهادکنندگان غیرصبور و پیشنهاد کنندگان افزایش دهنده کمیت. نتایج آزمایش نشان می دهند که برای اولین نوع پیشنهاد دهندگان، پیشنهاد در مورد قیمت های بالا برای دستیابی سریع به منابع، بهتر است، ضمن اینکه نوع دوم پیشنهاد دهندگان دارای پیشنهاد بهتری با قیمت های کم و حفظ منابع در حال انتظار بودند.
در کار قبلی، ما نیز از حراجهای ترکیبی برای توزیع منابع محاسباتی در بین گروهی از کاربران استفاده نمودیم.
ما یک راهکار ارائه پیشنهاد تطبیقی را برای پیشنهاد دهندگان در بازارهای ایستا پیشنهاد می کنیم که در آن نسبت های عرضه و تقاضا در طول کل دوره حراج ثابت نگهداشته می شود.
پیشنهاد دهنده با اتخاذ این راهکار می تواند سودناخالص خود را به طور دائم بر اساس سابقه ارائه پیشنهادش تنظیم کند و در نتیجه با پیشنهاد مطلوب حتی با دانش قبلی همگرایی داشته باشد.
- آزمایشات
- حراجهای ترکیبی
در این مقاله، ما سناریویی را بررسی می کنیم که در آن صورت حراجهای ترکیبی پیشنهاد- مهر و موم شده قیمت – اول، برای توزیع منابع محاسباتی میان گروهی از کاربران به کار برده می شوند.
فرض کنید m نوع منابع تامین شده برای یک مدیر منبع (حراجگذار) به n کاربر (پیشنهاد دهنده) است.
برای هر نوع منبع j ∈ {1, 2, …,m} یا M، ظرفیت cj نشاندهنده کل تعداد واحدهایی هست که در اختیار می باشند.
در هر زمان در طول حراج، هر کاربر i ∈ {1, 2, …, n} ممکن است نیاز به انواع معینی از منابع داشته باشد تا وظیفه اخیر خویش را انجام دهد و برای هر نوع منبع j، حداکثر تعداد واحدهایی که می تواند برای dj می تواند نیاز داشته باشد، است.
وی می تواند پیشنهاد مهر و موم شده bi = (T, pi(T)) را بپذیرد به صورتی که
T = (t1, t2, …, tm) دسته یک منبع است، با tj که تعداد واحدهایی است که منبع j توسط i با تامین 0 ≤ tj ≤ dj , ∀j ∈ M درخواست می شود و pi(T) عدد مثبت نشاندهنده قیمت i است که برای بدست آوردن T پرداخت خواهد کرد.
بعد از دریافت پیشنهادات از سوی تمامی کاربران، مدیر منبع مسئله تعیین برنده را حل می کند که با
داده می شود. به صورتی که اگر پیشنهاد دهنده i به T تخصیص شده باشد، xi(T) = 1.
هر کاربر برنده i که pi(T) را می پردازد، به منابع دسترسی دارد و وظیفه خویش را انجام می دهد و دوباره کنترل دسترسی را به سمت مدیر منبع بازمی گرداند.
ما به فرایند شروع قبول پیشنهاد تا پایان برگشت کنترل دسترسی به عنوان یک دور حراج ترکیبی اشاره می کنیم.
از آنجائی که منابع مجددا قابل استفاده می باشند، حراج ترکیبی را می توان برای دورهای متعدد قبل از بسته شدن توسط مدیر حراج اجرا کرد.
ما برخی فرضیات به کار برده شده در این مقاله را فهرست می کنیم.
اولاً، فرض ما این است که اطلاعات قابل دسترس برای هر پیشنهاد دهنده اطلاعات پیشنهادات قبلی وی می باشد، برای مثال دسته های ارائه پیشنهاد، قیمت های پیشنهادی، و نتایج پیشنهاد بردها و ضررها. هر گونه اطلاعات سایر پیشنهاددهندگان منتشر نمی گردد.
ثانیا، فرض ما بر این است که بازار حراج ترکیبی استاتیک می باشد.
گفته می شود یک بازار حراج ترکیبی در صورتی استاتیک و ایستا است که نسبت های عرضه و تقاضا برای انواع مختلف منابع در طول کل فرایند حراج ثابت نگهداشته شوند.
در نهایت، ما فقط ساده ترین موردی را مورد توجه قرار می دهیم که هر پیشنهاد کننده فقط یک پیشنهاد واحد را در یک دور بپذیرد که این بدان معناست که هیچ زبان پیشنهادی به کار نمی رود.
برد دور قبلی پیشنهاد جدید را می پذیرد، ضمن اینکه هر بازنده به پذیرش پیشنهاد از دست رفته ادامه می دهد.
ولی، همین پیشنهاد در صورتی متوقف خواهد شد که برای دورهای پی در پی T پذیرفته شده باشد و به این معناست که پیشنهاد دهنده صبر کمی در انتظارکشیدن دارد.
3.2 یادگیری – Q
یادگیری – Q یک یادگیری تقویت کننده به کار رفته برای حل وظایف مدل سازی شده توسط فرایندهای تصمیم گیری مارکو می باشد.
با یادگیری یک تابع ارزش- حراج کار می کند که منفعت پیش بینی شده ای از انجام یک حراج خاص را در یک وضعیت معین ارائه کرده و پس از آن یک سیاست ثابت را دنبال می کند.
دو نقطه قوت یادگیری- Q این می باشند که میتوانند منفعت پیش بینی شده حراجهای مختلف را بدون مدل سازی محیط مقایسه کرده و می توانند به صورت آنلاین به کار برده شوند.
یادگیری- Q برای حل مسائله تصمیم گیری سلسله مراتبی مناسب می باشد به صورتی که منفعت های حراج به ترتیبی از تصمیمات اتخاذ شده بستگی دارد و در مورد دینامیک های محیط عدم قطعیت وجود دارد.
در چارچوب یادگیری- Q، محیطی که نماینده یا عامل با آن در تعامل است، یک وضعیت معین، زمان- مجزا، سیستم دینامیک اتفاقی می باشد.
تعامل میان نماینده و محیط در زمان t شامل ترتیب زیر می باشد:
- نماینده وضعیت st ∈ S را درک می کند.
- بر اساس وضعیت st، نماینده یک اقدام را در ∈A انتخاب می کند.
- با احتمال پذیری Prst,s∗t(at)، نماینده به وضعیت جدید s∗t ∈ S منتقل می کند.
- محیط به صورت نتیجه نماینده ای که در at st انتخاب می شود، پاداش r(st, at) دریافت می کند.
- پاداش r(st, at) مجددا به نماینده برگردانده می شود و فرایند تکرار می گردد.
هدف نماینده، تعیین سیاست مطلوب π∗ است که کل پاداش کسرشده را افزایش خواهد داد، که با
داده می شود.
به صورتی که E اپراتور پیش بینی است، 0 ≤ β < 1 ضریب کسرشده و π سیاست S → Aمی باشد. اغلب تابع ارزش وضعیت s نامیده می شود.
یادآوری اینکه معادله 2 می تواند به این صورت نوشته شود:
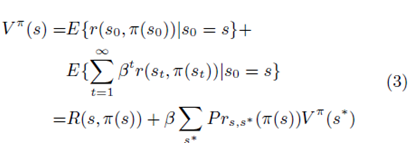
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
به صورتی که … معدل… می باشد. معادله 3 نشان می دهد که تابع ارزش وضعیت s می تواند بر اساس پاداش فوری پیش بینی شده اقدام فعلی و تابع ارزش وضعیت بعدی نمایش داده شود.
بر اساس معیارهای بهینه بودن بلمن، همیشه یک سیاست مطلوب π∗ وجود دارد که معادله 3 را تامین می کند.
هدف، یافتن سیاست مطلوب بدون دانش قبلی در مورد R(s, π(s)) و Prs,s∗(π (s)) می باشد. برای یک سیاست π، یک ارزش Q به این صورت تعریف می شود:
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
که پاداش کسر شده پیش بینی شده برای اجرای اقدام a در وضعیت s و سپس سیاست دنبال شده πبعد از آن می باشد.
فرض کنید
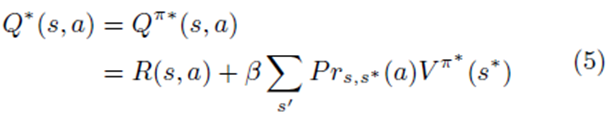
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
پس می توانیم بدست آوریم که
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
بنابراین تابع میزان مطلوب V ∗ را می توان از Q∗(s, a) بدست آورد و به نوبت Q∗(s, a) ممکن است به این صورت بیان شود
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
به صورتی که s∗ وضعیت جدید با احتمال پذیری Prs,s∗(a) هنگامی که کارa د روضعیت s انجام شود، حاصل می گردد.
فرایند یادگیری- Q در تلاش برای یافتن Q∗(s, a) به شکل برگشتی (s, a, s∗,R(s, a)) است و قاعده آن عبارتست از:
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
به صورتی که M = maxa∗ Q(s∗, a∗) و 0 ≤ α < 1 سرعت و میزان یادگیری است.
- راهکار ارائه پیشنهاد تطبیقی مبتنی بر یادگیری – Q
همانطور که در بخش فوق توضیح داده شد، هر برنده نیاز به پرداخت قیمتی که برای کسب منابع پیشنهاد می کند، داشته و هر بازنده هیچ مبلغی پرداخت نمی کند. سود پیشنهاددهنده i به این صورت محاسبه می شود:
ui(T) = _ vi(T) − pi(T) اگر i برنده شود، در غیراینصورت صفر می باشد.
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
به صورتی که ui(T), vi(R) و pi(T) ارزشیابی وی، منفعت سود وی و قیمت پیشنهادی وی برای دسته T می باشد.
با گذاشتن یک پیشنهاد برای یک دسته منبع، یک پیشنهاد دهنده منطقی از میزان مثبتی استفاده خواهد کرد که کمتر از ارزشگذاری وی برای آن دسته باشد، در غیراینصورت هنگام برد، سودمنفی کسب خواهد کرد.
باید گفت، اگر ارزشگذاری پیشنهاد دهنده i برای دسته T برابر باشد با vi(T)، پس قیمت پیشنهادی وی pi(T) برابر است با pi(T) =(1−pmi)×vi(T) به صورتی که 0 < pmi < 1.
ما در اینجا pmi را به عنوان سودناخالص پیشنهاد دهنده i مورد اشاره قرار می دهیم.
در ترکیب با معادله 9، از اینرو منفعت پیشنهاد دهنده i عبارتست از:
اگر i برنده شود ui(T) = _ pmi × vi(T) در غیراینصورت صفر می باشد.
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
حال، مسئله پیچیده ای وجود دارد که مورد مواجه یک پیشنهاد دهنده در زمینه تصمیم گیری در مورد سود حاشیه برای کاربرد هنگام ارائه پیشنهاد برای دسته های منبع می باشد:
ارائه پیشنهاد با حاشیه سود کم احتمال برد وی را افزایش خواهد داد، ولی سود برد وی را در همان زمان کاهش می دهد.
ارائه پیشنهاد با حاشیه سود بالا منجر به سود زیاد در برد می گردد، ولی خطر شکست بالایی نیز وجود دارد.
اگر پیشنهاد دهنده ای بتواند دانش قبلی در مورد محیط بازار کسب کند، برای مثال نسبت عرضه و تقاضا، ممکن است از این اطلاعات برای کمک به تصمیم گیری استفاده کند.
برای مثال، پیشنهاد دهنده ای که در مورد بازاری که عرضه های بیشتر منابع نسبت به تقاضا وجود دارد، دانش قبلی دارد، هنگام ارائه پیشنهاد از حاشیه سود بالا استفاده خواهد کرد.
به این خاطر است که در این نوع بازار، رقابت برسر منابع در بین پیشنهاد دهندگان شدید نیست و ارائه پیشنها با حاشیه سود بالا منجر به سود بالای برد می گردد، ضمن اینکه احتمال برد تقریبا تحت تاثیر قرار نمی گیرد.
ولی با فرض ما، اطلاعات قابل دسترس برای هر پیشنهاد دهنده بسیار محدود می باشد.
در اینجا، هدف ما طراحی یک راهکار ارائه پیشنهاد تطبیقی بر اساس اصل یادگیری-Q است به طوری که پیشنهاد دهنده ای که آن را اتخاذ می کند، می تواند به شکل زمانبندی حتی با اطلاعات محدود به بازار پاسخ داده و این نقش اصلی این کار می باشد.
- مفاهیم اصلی
ما ابتدا برخی مفاهیم اصلی به کار برده شده در راهکار ارائه پیشنهاد تطبیقی مبتنی بر یادگیری –Q را معرفی می کنیم.
تعریف1. ثبت ارائه پیشنهاد یک پیشنهاد b برای پیشنهاد دهنده i یک brb = (Tb, vi(Tb), pmb,waitb,winb) سه تایی است، به صورتی که Tb دسته درخواست شده در b، vi(Tb) ارزش گذاری i برای Tb، waitb تعداد دورهایی است که پیشنهاد دهنده برای انتظار قبل از اینکه bپذیرفته یا رد شود، نگهداشته شده است و winb عدد صحیح 0 یا 1 است که نشاندهنده نتیجه ارائه پیشنهاد برای b می باشد، در صورتی که b در نهایت پذیرفته شود، برابر با یک و در غیراینصورت صفر می باشد.
براساس این تعریف، می توان مشاهده کرد که حداکثر میزان waitb ، τ می باشد و حداکثر میزان برای آن صفر است.
در مورد قبلی، پیشنهاد دهنده برای دورهای T صبر میکند و در نهایت پیشنهاد را متوقف می کند و در مورد بعدی، پیشنهاد b، هنگام پذیرفته شدن از سوی پیشنهاددهنده در دور اول پذیرفته می شود.
به علاوه، میزان winb را نیز می توان بر اساس میزان waitb استنباط نمود، اینکه اگر و فقط اگر waitb = τ باشد، winb = 0.
تعریف 2. سابقه ارائه پیشنهاد یک پیشنهاد دهنده، که به صورت cbh_ بیان شده، ترتیب جدیدترین ثبت های پیشنهاد ρ است.
ولی، می گوییم که اگر و فقط اگر تمامی این ثبت های پیشنهاد ρ همان حاشیه سود را به اشتراک بگذارند، سازگار می باشد.
فرض کنید ρ > 1، هر بار زمانی که یک پیشنهاد پذیرفته یا رد شود، سابقه ارائه پیشنهاد به روز رسانی می شود که قدیمی ترین ثبت پیشنهاد از سابقه ارائه پیشنهاد حذف می شود و جدیدترین وارد سابقه ارائه پیشنهاد می گردد.
ولی، گفته می شود سابقه ارائه پیشنهاد تنها زمانی سازگار است که تمامی ثبت های ارائه پیشنهاد از حاشیه سود یکسان استفاده می کنند.
اگر پیشنهاد دهنده ای از یک حاشیه سود ثابت برای تمامی ثبت های ارائه پیشنهاد استفاده کندف پس هر سابقه سازگار می باشد؛
اگر وی هرگز از یک حاشیه سود یکسان برای دو ثبت ارائه پیشنهاد پی در پی استفاده می کند.
تعریف 3. وضعیت یک پیشنهاد دهنده، که با s نشان داده شده، حاشیه سودی است که اخیرا توسط این پیشنهاد کننده به کار رفته است.
در طول حراج، پیشنهاد کننده می تواند حاشیه سود خویش را یا با کاهش یا با افزایش تغییر دهد که گذر از وضعیت وی را هدف قرار خواهد داد.
تعریف 4. اقدام یک پیشنهاد دهنده در وضعیت s که با a نشان داده شده ، عدد واقعی غیرصفر است که توسط آن وضعیت وی از s برای دسته های زیر قبل از عبور به s to s∗ = s +a عبور خواهد کرد، به صورتی که وضعیت s∗ تامین کننده 0 < s∗ < 1 است.
بر اساس تعریف، می توان مشاهده کرد که هر بار که اقدام a در وضعیت s انجام می شود، به خاطر ویژگی غیرصفر a پیشنهاد کننده به وضعیت s∗ عبور می کند، به این معناست که پیشنهاد دهنده حاشیه سود جدیدی را برای دورهای زیر قبل از عبور بعدی با محدودیت 0 < s∗ < 1 استفاده خواهند کرد.
تعریف 5. پاداشی که یک پیشنهاد کننده از محیط هنگام انجام اقدام a در وضعیت s دریافت می کند، به صورت r(s, a) بیان شده که به این صورت تعریف می شود:
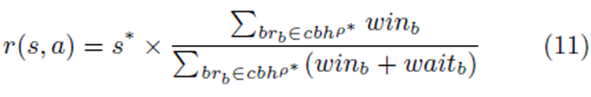
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
به صورتی که s∗ هنگام انتخاب وضعیت a در وضعیت جدید s است و
سابقه ارائه پیشنهاد سازگار ایجاد شده در زمانی است که پیشنهاد دهنده در وضعیت s∗ باقی می ماند.
- الگوریتم اصلی
بر اساس مفاهیم اصلی تعریف شده فوق، الگوریتم اصلی راهکار تطبیقی مبتنی بر یادگیری – Q را توصیف خواهیم نمود.
ایده اصلی این است که هر باز که سابقه ارائه پیشنهاد سازگاری ایجاد می گردد، پیشنهاد دهنده پاداش را محاسبه کرده، مقادیر- Q را ارزیابی می کند. و یک اقدامی را بر اساس مقادیر-Q به روز رسانی شده انتخاب می کند.
با انجام این کار به صورت تکراری، پیشنهاد دهنده در بین وضعیت های مختلف عبور خواهد کرد و در نتیجه به وضعیت بهینه می رسد که منفعت جمع شده پیشنهاد دهنده را در دراز مدت افزایش می دهد. ما ابتدا تعریف آن را ارائه می کنیم.
بیان 1. می گوییم که وضعیت s ، که به صورت s <_ s∗, بیان شده، اگر و فقط اگر |s − s∗| < θنزدیک به وضعیت s∗،θ می باشد.
تعریف 6. میزان- Q جفت وضعیت مجموعه – اقدام (L,a) به صورتی که L ⊆ S، به صورت میانگین مقادیر-Q جفت (s, a) تعریف می شود، به صورتی که s ∈ L. یعنی:
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
راهکار تطبیقی در الگوریتم 1 بیان می شود. ما از s برای بیان وضعیت فعلی پیشنهاد دهنده که با انجام عمل a′ در وضعیت s′ بدست آمده و از s∗ برای بیان وضعیت بعدی استفاده می کند، در صورتی که اقدام a′ بر روی s انجام می گیرد، استفاده می کنیم.

ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
ما نیز هنگام رسیدن به وضعیت s′ و s، r و r′ را برای بیان پاداش بدست امده توسط پیشنهاد دهنده به کار می بریم.
به علاوه، از متغیر VQ(s,a) برای نشان دادن تعداد مواقعی استفاده می کنیم که جفت وضعیت- اقدام (s, a) بازدید شده است و با شروع الگوریتم با 0 آغاز می شود.
راهکار تطبیقی در الگوریتم 1 بیان می شود. در ابتدا، مجموعه وضعیت s و مجموعه اقدام A به ترتیب با {sini} و {+θ, −θ} آغاز می شوند و سپس برخی متغیرهای به کار برده در الگوریتم نیز شروع می شوند (خط 1 و 2).
در طول فرایند حراج، پیشنهاد دهنده در وضعیت فعلی s و گذر به وضعیت جدید هر زمان که 1) سابقه پیشنهاد سازگار جدید با طول ρ تشکیل می شود و 2) θ بیش از میزان آستانه ǫ است، باقی می ماند.
ابتدا پیشنهاد دهنده پاداش جفت وضعیت- اقدام قبلی r(s′, a′) را بر اساس معادله 11 (خط 6) را محاسبه کرده و سپس مقادیر-Q را برای زوجهای (s′, a′) و (s, a′) با استفاده از معادلات زیر به روز رسانی می کند (خطوط 7 و8):
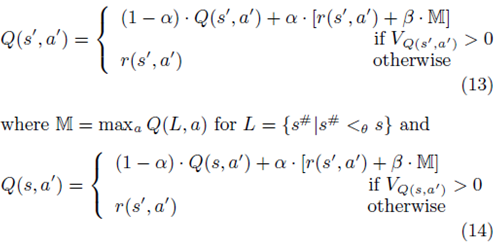
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
توجه داشته باشید که ما مقدار Q(s, a′) را که متغیری از q قبل از بروز رسانی می باشد، ذخیره می کنیم. این به خاطر آن است که r(s′, a′) باید برای بروز رسانی Q(s′, a′) بکار رود تا Q(s, a′).
به روز رسانی Q(s, a′) با r(s′, a′) به این معناست که ما بر مبنای تجربه معتقدیم که انجام اقدام a′ در وضعیت s همان میزان پاداش را به اندازه انجام حراج a′ در وضعیت s′ ایجاد خواهد کرد.
Q(s, a′) به روز رسانی شده برای تصمیم گیری در مورد وضعیت s، که بعد از ان برای میزان اصلی q بازیابی می شود، مورد استفاده قرار خواهد گرفت (خط 26).
پس پیشنهاد کننده وضعیت کاهش را برای θ بررسی کرده و میزان آن را در صورت لزوم کاهش می دهد (خط 9 تا 14) و در صورتی که هر دو زوج اقدام – وضعیت (s, a′) و (s,−a′) قبلا بازدید شده باشند، یک اقدام را بر اساس قوانین زیر (خط 15 تا 25):I) انتخاب می کندو پیشنهاد کننده اقدامی را با میزان بیشتر Q انتخاب خواهد کرد؛ 2) هیچ یک از آنها قبلا بازدید نشده است و به این معناست که θ فقط کاهش یافته است، پیشنهاد کننده ابتدا اقدامی را با فرض کاهش θ که اتفاق نیفتاده است، انتخاب می کند و سپس، اقدام انتخاب شده را با y کاهش می دهد؛ 3) اگر r ≥ r′ ، در غیراینصورت به این معناست که انجام اقدام a′ منجر به افزایش پاداش شده است و سپس به این اقدام ادامه می دهیم؛ در غیراینصورت، اگر r < r′ به این معناست که انجام اقدام a′ منجر به کاهش پاداش می گردد و ما سپس، عکس این اقدام عمل می کنیم.
بعد از ان، پیشنهاد دهنده بر اساس اقدام انتخاب شده (خط 27) به وضعیت جدید عبور کرده و مجموعه وضعیت S را در صورت لزوم به روز رسانی می کند (خط 28 تا 30) و تابع فراخوانی مقادیر-Q FillUp (خط 31) که با آنعبور از وضعیت به اتمام رسیده است.
چنین عبوری تا زمانی که θ کوچکتر از میزان آستانه ǫ است، تکرار خواهد شد که بعد از آن پیشنهاد دهنده برای تمامی دورهای بعدی تا اتمام حراج در آن وضعیت باقی خواهد ماند.
سپس، ما دو تابع Decreaseθ و FillUpQValues را به تفصیل معرفی خواهیم کرد.
- تابع کاهش
میزان θ برای اطمینان از اینکه وضعیت پیشنهاد کننده می تواند به وضعیت بهینه برسد، کاهش داده می شود.
تعریف 7. سابقه وضعیت که به صورت sh نشان داده شده، ترتیبی از اعداد واقعی λ است که در ان عامل kاُم، shk، جدیدترین وضعیت kاُم پیشنهاددهنده می باشد.
تعریف 8. سابقه θ، که به صورت θh نشان داده شده، ترتیبی از اعداد واقعی λ است که در ان عامل kاُم θhk می باشد، عمل به کار برده شده زمانی است که پیشنهاد دهنده از shk−1 به shk عبور میکند.
بیان 2. می گوییم که s ⇒ π اگر 1) s < π و عمل بعدی پیشنهاد دهنده a > 0 یا 2) s > π و عمل بعدی پیشنهاد دهنده a < 0.
تابع Decreaseθ در الگوریتم 2 داده می شود. ابتدا، ما معدل میزان عناصر را در sh (خط 1) محاسبه کرده و برای هر عامل بررسی می کنیم که آیا فاصله بین shk و معدل بیشتر از θhk نیست و از 0 یا 1 متغیر ωk برای نشان دادن نتیجه (خط 2 تا 7) استفاده می کند یا نه . در تصمیم گیری برای کاهش θ، سه وضعیت را بررسی می کنیم (خط 8):
ابتدا بررسی می شود که آیا حداقل عوامل φ در sh بر اساس عمل انتخاب شده نزدیک به میزان متوسط می باشد یا نه، سپس بواسطه آن معدل را به عنوان تخمین وضعیت مطلوب مورد توجه قرار می دهیم و موارد دوم و سوم با هم تضمین می کنند که وضعیت مطلوب می تواند در صورتی حاصل شود که θ کاهش یابد. اگر تمامی شرایط صدق کنند، واقعیت برمی گردد.
تابع الگوریتم 2: کاهش

ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
- تابع مقادیر FillUpQ
همانطور که از نامش برمی آید، ما مقادیرQ را در این تابع بر اساس سایر مقادیر در ماتریس Q برای برخی جفت های وضعیت- عمل پر می کنیم.
این به خاطر آن است که بر اساس تعریف ما از پاداش در معادله 11، برای دو جفت عمل- وضعیت (s1, a1) و (s2, a2)، پاداشهای آنها، و نیز مقادیر Q آنها در صورت ترکیب با تعریف در معادله 7، باید هنگامی که ρ∗ به طور نامحدود بزرگ باشد، در صورتی که s1 + a1 = s2 + a2، یکسان باشد.
به علاوه، مقادیر Q برای برخی جفت ها باید نزدیک به برخی دیگر باشد، برای مثال، با وجود اینکه 0.8 + 0.04 6= 0.75 + 0.1، مقادیر Q برای جفت های وضعیت- عمل (0.8, 0.04) و (0.75, 0.1) بایستی نزدیک به یکدیگر باشند.
بر اساس ایده های فوق، ما تابع FillUpQValues را در الگوریتم 3 بیان می کنیم.
برای هر وضعیت در s ∈ S و هر عمل در a ∈ A، اگر مقدار-Q آن Q(s, a) قبلا دیده نشده باشد، پس ما مجموعه وضعیتی را بررسی می کنیم که عوامل ان θ نزدیک به s+a (خط 4) می باشند.
اگر مجموعه وضعیت خالی نباشد، ما ابتدا مقدار-Q هر جفت عمل- وضعیت (s, a) را با این میزان از جفت مجموعه – عمل (L, a) (خط 6) تخمین زده و سپس مقدار VQ(s,a) را با 1 (خط 7) اضافه می کنیم.

ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
- شبیه سازی ها
برای ارزیابی عملکرد راهکار تطبیقی بر اساس یادگیری-Q، ما دو مجموعه آزمایش انجام دادیم.
در مجموعه اول آزمایشات، ما راهکار مطلوب را در انواع مختلف بازار با مجموعه ای از شش راهکار تخمین می زنیم. یک راهکار ثابت راهکاری است که پیشنهاد دهنده را در یک وضعیت یکسان باقیمانده در طول فرایند حراج حفظ می کند.
در مجموعه دوم آزمایشات، ما عملکردهای راهکار تطبیقی (AS)، راهکار تطبیقی بر اساس یادگیری –Q (Q-AS)، راهکار تصادفی (RS)، و راهکار مطلوب (OPT) مقایسه می کنیم.
راهکار تطبیقی راهکاری است که ما در کار قبلی خویش پیشنهاد کرده ایم که نیاز به نتایج خوبی در بازارهای مختلف دارد.
راهکار تصادفی راهکاری است که پیشنها دهنده را میان وضعیت های متفاوت برای ثبت های ارائه پیشنهاد متفاوت به طور تصادفی عبور می دهد.
راهکار مطلوب راهکاری است که بر اساس نتایج اولین مجموعه آزمایشان به طور مصنوعی ایجاد شده است.
همانطور که راهکار تطبیقی نیز در بازارهای مختلف خوب عمل می کند، ما راهکار تطبیقی و راهکار تطبیقی مبتنی بر یادگیری –Q را به تفصیل مقایسه می کنیم.
به علاوه، فرایند همگرایی وضعیت پیشنهاد دهنده ای که از راهکار تطبیقی مبتنی بر یادگیری –Q استفاده میکند، نشان می دهیم.
- اجرای آزمایش
در آزمایشات خویش، هر حراج ترکیبی برای 500 دور تکرار می شود و یک تکرار 500 دور به صورت یک دور تلقی می گردد.
ما در هر دور، با انگیزه گرفتن از کارهای دیگر، یک پیشنهاد کننده آزمایش با استفاده از راهکار X داریم و بقیه ارزشگذاری های واقعی شان را پیشنهاد می کنند.
در اینجا، X می تواند راهکار تطبیقی، راهکار تصادفی، راهکار تطبیقی مبتنی بر یادگیری –Q ، یا راهکار مطلوب باشد.
عملکردهای راهکارهای متفاوت از طریق سود های جمع شده پیشنهاد دهنده تست در 100 دور مقایسه می شوند.
مجموعه های این آزمایشات به این صورت می باشند. گروهی از n = 60 برای m = 4 نوع منابع فراهم شده توسط تامین کننده منبع مقایسه می شوند.
برای هر پیشنهاد کننده، تعداد واحدهایی که می توانند برای منابع مختلف درخواست کنند، اعداد صحیح تصادفی برداشته شده از توزیع های یکدست [0, 3]، [0, 2], [0, 2] و [0, 1] می باشند.
در ابتدای هر دور، هر پیشنهاد دهنده ارزشیابی های خویش را از دسته های منبع آغاز می کند.
ارزشگذاری های وی برای واحد مجزای منابع مختلف اعداد واقعی برداشته شده تصادفی از توزیع های یک شکل [3, 6]، [4, 8], [4, 8] و [6, 10] می باشند.
برای یک دسته منبع T، که حاوی بیش از یک نوع منبع است، بذر همکاری، syn(T) از توزیع یکدست 0.2, 0.2] [ برداشته می شود و ارزشگذاری وی برای آن دسته محصول مجموع ارزش گذاری های منابع واحد و 1 + syn(T) می باشد.
بذر همکاری مثبت به معنای وجود مکمل هایی میان منابع و بذر همکاری منفی به معنای وجود قابلیت جایگزینی در بین آنها می باشد.
در محیط های ما، از آنجائی که کل تقاضاهای کاربران ثابت می باشند، ما تامین کنندگان منابع را اصلاح نموده و عامل ظرفیت cf را برای نشان دادن انواع مختلف بازار بیان می کنیم:اگر نسبت کل عرضه ها و تقاضاها در بازار برابر با cf : 1 باشد، می گوییم این یک بازار cf : 1 است.
برای مثال، وقتی ظرفیت های منابع 90, 60, 60 و 30 می باشند، کل عرضه ها و تقاضاهای پیش بینی شده برابر هستند. در این صورت، می گوییم که بازار یک بازار 1 : 1 است.
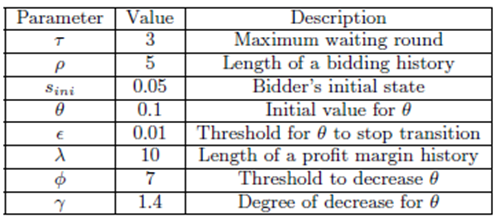
پارامترهای به کاربرده شده در شکل 1 نشان داده می شوند.
به علاوه، ما از میزان ثابت یادگیری α = 0.2 و نرخ تنزیل شده β = 0.1 استفاده می کنیم.
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
شکل 1. پارامترهای به کار رفته در آزمایشات
- نتایج آزمایش و تحلیل
در مجموعه اول آزمایشات، هدف ما تخمین راهکار مطلوب در انواع مختلف بازار با مجموعه ای از راهکارهای ثابت می باشد.
در اینجا، از 19 راهکار ثابت مختلف استفاده می کنیم که در آن وضعیت پیشنهاد کننده در s1, s2, … s19 حفظ می شود، به صورتی که sl = l × 0.05 for l = 1, 2, …19.
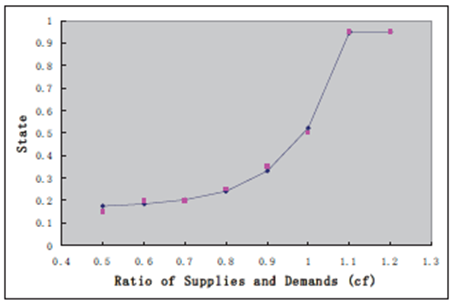
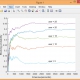
شکل 2 نتایج را برای اولین مجموعه از آزمایشات نشان می دهد.
هر نقطه قرمز نشان دهنده راهکار ثابتی است که در آن نوع بازار مثل نقطه قرمز (0.7, 0.2) به نحو احسن فعالیت می کند، یعنی اینکه در بازار 0.7 : 1، راهکار ثابت که پیشنهاد دهنده را در وضعیت 0.2 قرار می دهد، در بین تمامی راهکارهای ثابت عالی عمل می کند.
بر اساس این شکل، می توان مشاهده کرد که هر چه رقابت بازار برای مصرف کنندگان منبع کمتر باشد، ارزش وضعیتی که آن پیشنهاد دهنده در آن نگهداشته می شود، بیشتر است.
برای مثال، در بازار1.2 : 1، در صورتی که پیشنهاد دهندگان با رقبای کوچکی مواجه شوند، راهکاری که وضعیت پیشنهاد دهنده در 0.95 نگهداشته شود، به خوبی عمل می کند؛ ضمن اینکه در بازار0.5 : 1، در صورتی که پیشنهاد دهندگان با رقبای بسیار کمی از بازارهای دیگر مواجه شوند، راهکاری که وضعیت پیشنهاد دهنده در 0.15 نگهداشته شود، بسیارخوب عمل می کند.
این مطابق با درک مستقیم ما است که در بازار با رقابت کم، باقی ماندن در وضعیتی با حاشیه سود بالا برای کسب سود بیشتر بهتر است، ضمن اینکه در بازار با رقابت کامل، برای او بهتر است که در وضعیتی با حاشیه سود کمی برای شکست دادن دیگران بماند.
بر اساس این نقاط قرمز، ما راهکارهای مطلوب را در بازارهای مختلف با یک شیوه رگرسیون برآورد می کنیم.
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
شکل 2. برآورد راهکار مطلوب
از تابع تکه یی sopt(cf) برای تطبیق با نقاط قرمز استفاده می کنیم که با
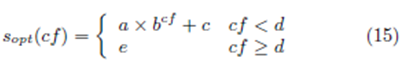
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
داده می شود.
نتیجه رگرسیون این است که 2561.574, c = 0.1683, e = 0.95 and d = 1.109873 a = 0.0001382, b = که در شکل 2 با خط آبی نشان داده شده است.
می توان مشاهده کرد که نقاط قرمز به خوبی تطبیق می کند، و در زیر،در صورت صحبت در مورد بازاری با نوع cf، میزان تابع را به صورت وضعیت مطلوب مورد استفاده قرار خواهیم داد.
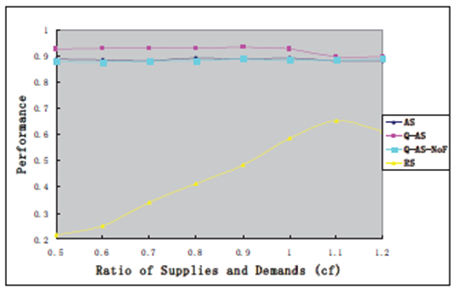
شکل 3 نتایج مجموعه دوم آزمایشات را نشان می دهد. در اینجا، عملکردهای سه راهکار مختلف دیگر از طریق نسبت سودهای جمع آوری شده حاصل از آنها و سودهای بدست آمده با راهکار مطلوب ایجاد شده بر اساس معادله 15 مقایسه می شوند.
توجه داشته باشید که در معادله 15، حداکثر میزان برای وضعیتی که پیشنهاد دهنده بتواند باقی بماند، 0.95 است، پس برای انجام مقایسه عادلانه، ما نیز همین محدوده بالایی 0.95 را برای این سه راهکار اجرا می کنیم.
بر اساس شکل 3، می توان مشاهده کرد که هر دو راهکار تطبیقی و راهکار تطبیقی بر اساس یادگیری- Q به خوبی عمل می کند و راهکار تصادفی در محیطهای متفاوت بازار بسیار خوب می باشد.
راهکار تطبیقی مبتنی بر یادگیری –Q دارای ارتقا در عملکردها برای راهکار تطبیقی از 2% تا 5% می باشد.
همانطور که توصیف شد، راهکار مطلوب بر اساس مجموعه راهکارهای تثبیت شده مصنوعی ایجاد شد، بنابراین پیشنهاد دهنده با استفاده از این راهکار م یتواند به عنوان دارنده دانش قبلی در مورد محیط بازار تلقی گردیده و قادر به باقی ماندن در وضعیت مطلوب برای بدست آوردن سود بالا می باشد.
بر عکس، پیشنهاد دهنده با استفاده از راهکار تصادفی می تواند به عنوان عدم دارا بودن هر گونه دانش قبلی در مورد بازار تلقی گردیده و در بین وضعیت های متفاوت برای ثبت های متفاوت ارائه پیشنهاد عبور کند.
از اینرو، مسئله مهمی است که عملکردهای راهکار تطبیقی و راهکار تطبیق مبتنی بر یادگیری- Q بتواند بیش از 90% راهکار مطلوب در محیط های مختلف بازار باشد.
همانطورکه پیشنهاد کننده ای با استفاده از راهکار تطبیقی یا راهکار تطبیقی مبتنی بر یادگیری –Q نیاز به شناخت نوع بازار از قبل ندارد، می توان این نتیجه گیری را ارائه کرد که پیشنهاد کننده با استفاده از راهکار در بازارهای مختلف به خوبی عمل می کند، حتی بدون هیچ دانش قبلی.
برای جستجوی دلیل اینکه راهکار مبتنی بر یادگیری- Q راهکار تطبیق را به خوبی اجرا می کند، ما آزمایش زیر را انجام دادیم.
عملکردهای راهکار دیگر Q-AS-NoF را که شبیه به راهکار تطبیقی مبتنی بر یادگیری –Q است، آزمایش می کنیم به استثنای اینکه ما تابع FillUpQValues را در الگوریتم (خط 31) فراخوانی نمی
ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
شکل 3. سودهای حاصله از پیشنهاد کننده تست با استفاده از راهکارهای AS, Q-AS و RS
کنیم و عملکرد آن را با خط سبز در شکل 3 نشان می دهیم.
ما با یادآوری الگوریتم راهکار تطبیقی، می بینیم که همان اصل را با Q-AS-NoF ولی با تفاوتهای اندک به اشتراک می گذارد. و همچنین منطقی است که با Q-AS-NoF به طور قابل مقایسه عمل کند.
با خلاصه سازی نتایج فوق، می توانیم به این نتیجه گیری برسیم که تابع FillUpQValues در ارتقای راهکار تطبیقی مبتنی بر یادگیری-Q بر عملکرد راهکار تطبیقی که با آن پیشنهاد دهنده انتخاب های صحیحی را در اقدام خویش بر اساس اطلاعات تاریخی انجام می دهد، نقش اساسی دارد.
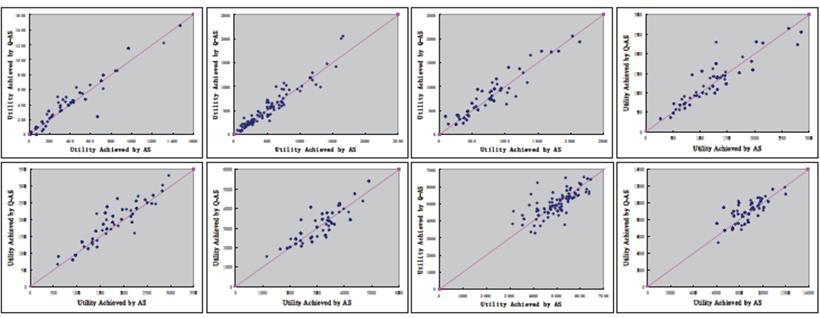
همچنین عملکردهای راهکار تطبیقی و راهکار تطبیقی مبتنی بر یادگیری –Q را در هر دور در هشت نوع بازار از 0.5:1 تا 1.2:1 مقایسه می کنیم که نتایج آن در شکل 4 نشان داده شده اند.
برای هر نوع بازار، خط قرمز مورب خطی است که نقطه روی ان به معنای عملکردهای راهکار تطبیقی و راهکار تطبیقی مبتنی بر یادگیری-Q یکسان می باشند و مختصات – X و مختصات –Y سودهای حاصله از پیشنهاد دهنده تست با استفاده از راهکار تطبیقی و راهکار تطبیقی مبتنی بر یادگیری –Q می باشد.
بر اساس شکل 4، می توان مشاهده کرد که برای هر نوع بازار، نقاطی که در قسمت سمت چپ خط هستند، بیش از نقاطی هستند که در سمت راست می باشند که این بدان معناست که در بسیاری از موارد، عملکرد راهکار تطبیقی مبتنی بر یادگیری – Q بهتر از راهکار تطبیقی می باشد.
ولی، مواردی همچنان هستند که در آنها راهکار تطبیقی راهکار تطبیقی مبتنی بر یادگیری- Q را اجرا می کند، که نیاز به بررسی های ببیشتری در کارهای آینده دارد.
شکل 4: مقایسه Q-AS و AS در یک دور واحد در بازارهای مختلف
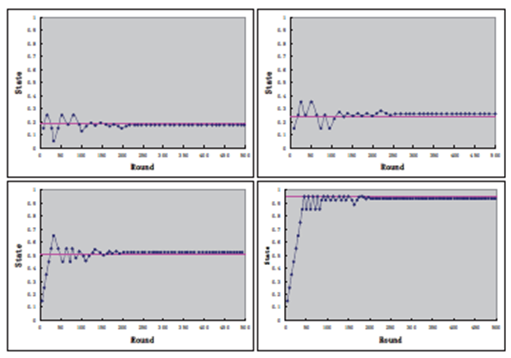
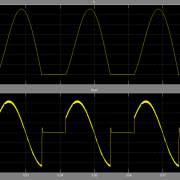
به علاوه، ما نیز فرایند همگرایی معمول وضعیت پیشنهاد کننده ای را نشان می دهیم که از راهکار تطبیقی مبتنی بر یادگیری- Q در یک دور واحد در چهار نوع بازار استفاده می کند: 0.6:1, 0.8:1, 1.0:1 و 1.2:1.
برای هر نوع بازار، خط افقی نشان دهنده وضعیت مطلوبی است که پیشنهاد کننده بایستی در این نوع بازار باقی بماند. بر اساس شکل5، میتوان مشاهده کرد که برای هر نوع بازار، وضعیت حفظ شده راهکار تطبیقی مبتنی بر یادگیری –Q در نهایت با وضعیت بهینه در آن نوع بازار همگرایی داشته است به این معنا که راهکار تطبیقی مبتنی بر یادگیری – Q قادر به یادگیری و تطبیق در بازارهای مختلف می باشد.
به علاوه، سرعت همگرایی زیاد است: برای
شکل 5. فرایند همگرایی معمول وضعیت پیشنهاد دهنده در یک دور واحد در بازارهای مختلف
هر نوع بازار، وضعیت پیشنهاد کننده تست تا حدود دور صدم همگرایی یافته است.
پیشنهاد کننده در ان وضعیت دورهای بعدی را حفظ می کند.
که راهکار تطبیقی مبتنی بر یادگیری – Q را تضمین کند که بتواند در مقایسه با راهکار مطلوب یک سودمندی بسیار خوبی ایجاد نماید.
- نتیجه گیری ها
در این مقاله، ما یک راهکار تطبیقی مبتنی بر یادگیری- Q را در حراجهای ترکیبی پیشنهاد می کنیمو پیشنهاد کننده این راهکار را می تواند برای انتقال و عبور از میان وضعیت های مختلف براساس سوابق پیشنهاد و در نهایت همگرایی با وضعیت مطلوب اتخاذ نماید.
نتایج آزمایش نشان می دهند که
1) راهکار تطبیقی مبتنی بر یادگیری- Qدر مقایسه با سایر راهکارهای مطلوب خوب عمل کرده و راهکار تطبیقی و راهکار تصادفی در محیطهای مختلف بازار را برتر عمل می کند.
2) پیشنهاد کننده با استفاده از راهکار تطبیقی مبتنی بر یادگیری –Q می تواند سود بالایی را در مقایسه با سود بدست امده از طریق راهکار مطلوب حتی بدون هیچ دانش قبلی در مورد بازار، کسب کند.
3) پیشنهادکننده با استفاده از راهکار تطبیقی مبتنی بر یادگیری- Q قادر به یادگیری و تطبیق می باشد و سرعت همگرایی بالا است.
علاوه بر ارزش گذاری های تجربی بسیار گسترده تر، این کار می تواند در جهات متعدد زیر بسط یابد.
اولاً، با اینکه راهکار تطبیقی مبتنی بر یادگیری- Q برتر از راهکار تطبیقی عمل می کند، همچنان مواردی هستند که در آن راهکار تطبیقی بهتر عمل می کند.
ما به جستجوی چنین وضعیت هایی علاقمند بوده و در تلاش هستیم تا راهکار تطبیقی مبتنی بر یادگیری را ارتقا دهیم.
ثانیاً، در این کار، از مقدار ثابت برای سرعت یادگیری و نرخ تنزل استفاده می کنیم.
مرحله بعدف در صدد تطبیقی ساختن آنها در الگوریتم خویش می باشیم به صورتی که تطبیقی مبتنی بر یادگیری –Q میتواند در بازارهای دینامیک به کار برده شود، به صورتی که ظرفیت های منابع و تعداد پیشنهاد دهندگان طی زمان متغیر می باشند.
جهت دیگر این است که ، همانطور که در فوق اشاره شد، راهکار تطبیقی مبتنی بر یادگیری- Q محدود به حراجهای ترکیبی نمی باشد.
در واقع، برای هر نوع حراج، ممکن است حتی به طور کلی تر، هر نوع بازی تکراری، این راهکار بتواند به بازیکن کمک کند تا به طور استراتژیک رفتار کرده و اگر تابع پاداش به طور مناسب تعریف شده باشد، عملکرد خوبی در بازی داشته باشد.
در آینده ما به کاربرد این راهکار درنوع دیگر حراج پرداخته و عملکرد آن را تحلیل می کنیم.
در نهایت، در این مقاله، از مدل نماینده – واحد استفاده می کنیم که به معنای این است که فقط یک پیشنهاد کننده از راهکار تطبیقی مبتنی بر یادگیری-Q استفاده نموده و دیگران راهکارهایشان را تثبیت می نمایند.
مسئله جالب این است که وقتی پیشنهاد دهندگان بیشتری از این راهکار به طور همزمان استفاده کرده باشند، چه مسئله ای اتفاق خواهد افتاد.
حدس ما این است که وقتی تمامی پیشنهاد دهندگان این راهکار را اتخاذ می نمایند، موازنه Nash صورت خواهد گرفت.
منابع:
[1] N. An, W. Elmaghraby, and P. Keskinocak. Bidding
strategies and their impact on revenues in
combinatorial auctions. Journal of Revenue and
Pricing Management, 3(4):337–357, 2005.
[2] A. Archer, C. Papadimitriou, K. T. Tardos, and J. H.
Foundation. An approximate truthful mechanism for
combinatorial auctions with single parameter agents.
In In Proc. 14th Symp. on Discrete Alg. ACM/SIAM,
pages 205–214, 2003.
[3] L. Ausubel, P. Cramton, R. McAfee, and J. McMillan.
Synergies in Wireless Telephony: Evidence from the
Broadband PCS Auctions. Journal of Economics &
Management Strategy, 6(3):497–527, 1997.
[4] L. M. Ausubel, P. Cramton, and P. Milgrom. The
clock-proxy auction: A practical combinatorial auction
design. Technical report, 2004.
[5] V. Avasarala, H. Polavarapu, and T. Mullen. An
approximate algorithm for resource allocation using
combinatorial auctions. In IAT ’06: Proceedings of the
IEEE/WIC/ACM international conference on
Intelligent Agent Technology, pages 571–578,
Washington, DC, USA, 2006. IEEE Computer Society.
[6] R. BELLMAN. Dynamic Programming. Princeton
University Press, 1957.
[7] M. Berhault, H. Huang, P. Keskinocak, S. Koenig,
W. Elmaghraby, P. Griffin, and A. Kleywegt. Robot
exploration with combinatorial auctions. Intelligent
Robots and Systems, 2003. Proceedings. 2003
IEEE/RSJ International Conference on, 2, 2003.
[8] R. Buyya, J. Giddy, and H. Stockinger. Economic
models for resource management and scheduling.
pages 1507–1542. Wiley Press, 2002.
[9] S. Clearwater. Market-Based Control: A Paradigm for
Distributed Resource Allocation. World Scientific, 1996.
[10] P. Cramton, Y. Shoham, and R. Steinberg.
Combinatorial Auctions. MIT Press, Cambridge,
Massachusetts, 2006.
[11] S. de Vries and R. Vohra. Combinatorial Auctions: A
Survey. INFORMS Journal On Computing,
15(3):284–309, 2003.
[12] I. Foster. The Anatomy of the Grid: Enabling Scalable
Virtual Organizations. Euro-Par 2001 Parallel
Processing: 7th International Euro-Par Conference,
Manchester, UK, August 28-31, 2001: Proceedings.
[13] Y. Fujishima, K. Leyton-Brown, and Y. Shoham.
Taming the computational complexity of
combinatorial auctions: Optimal and approximate
approaches. Proceedings of the Sixteenth International
Joint Conference on Artificial Intelligence, pages
548–553, 1999.
[14] A. Holland and B. O’Sullivan. Truthful risk-managed
combinatorial auctions. In IJCAI, pages 1315–1320,
2007.
[15] H. H. Hoos and C. Boutilier. Solving combinatorial
auctions using stochastic local search. In In
Proceedings of the Seventeenth National Conference on
Artificial Intelligence, pages 22–29, 2000.
[16] L. P. Kaelbling, M. L. Littman, and A. W. Moore.
Reinforcement learning: a survey. Journal of Artificial
Intelligence Research, 4:237–285, 1996.
[17] V. Krishna. Auction Theory. Academic Press, 2002.
[18] R. Lavi and N. Nisan. Towards a characterization of
truthful combinatorial auctions. pages 574–583, 2003.
[19] D. Lehmann, L. I. O’callaghan, and Y. Shoham. Truth
revelation in rapid, approximately efficient
combinatorial auctions. In Proceedings of the ACM
Conference on Electronic Commerce (ACM-EC),
pages 96–102, 1999.
[20] R. Mailler, V. Lesser, and B. Horling. Cooperative
negotiation for soft real-time distributed resource
allocation. In AAMAS ’03: Proceedings of the second
international joint conference on Autonomous agents
and multiagent systems, pages 576–583, New York,
NY, USA, 2003. ACM.
[21] N. Nisan and A. Ronen. Computationally feasible vcg
mechanisms. In In ACM Conference on Electronic
Commerce, pages 242–252. ACM Press, 2000.
[22] D. Parkes and L. Ungar. Iterative combinatorial
auctions: Theory and practice. Proceedings of the
National Conference on Artificial Intelligence, pages
74–81, 2000.
[23] S. Rassenti, V. Smith, and R. Bulfin. A combinatorial
auction mechanism for airport time slot allocation.
Bell Journal of Economics, 13(2):402–417, 1982.
[24] B. Rastegari, A. Condon, and K. Leyton-Brown.
Stepwise randomized combinatorial auctions achieve
revenue monotonicity. In ACM-SIAM Symposium on
Discrete Algorithms (SODA), pages 738–747, 2009.
[25] M. Rothkopf, A. Pekec, and R. Harstad.
Computationally Manageable Combinational
Auctions. Management Science, 44(8):1131–1147,
1998.
[26] T. Sandholm. An implementation of the contract net
protocol based on marginal cost calculations.
Proceedings of the National Conference on Artificial
Intelligence, pages 256–262, 1993.
[27] T. Sandholm, S. Suri, A. Gilpin, and D. Levine.
CABOB: A Fast Optimal Algorithm for Winner
Determination in Combinatorial Auctions.
Management Science, 51(3):374–390, 2005.
[28] M. Schwind, T. Stockheim, and O. Gujo. Agents’
bidding strategies in a combinatorial auction
controlled grid environment. In TADA/AMEC, pages
149–163, 2006.
[29] X. Sui and H.-F. Leung. An adaptive bidding strategy
in multi-round combinatorial auctions for resource
allocation. 20th IEEE International Conference on
Tools with Artificial Intelligence., 2:423–430, 2008.
[30] R. Sutton and A. Barto. Reinforcement Learning: An
Introduction. MIT Press, Cambridge, MA, 1998.
[31] C. Watkins. Learning from delayed rewards. In PhD
Thesis University of Cambridge, England, 1989.
[32] C. J. C. H. Watkins and P. Dayan. Technical note
q-learning. Machine Learning, 8:279–292, 1992.
[33] M. Yokoo, T. Matsutani, and A. Iwasaki.
False-name-proof combinatorial auction protocol:
Groves mechanism with submodular approximation.
In AAMAS, pages 1135–1142, 2006.
[34] E. Zurel and N. Nisan. An efficient approximate
allocation algorithm for combinatorial auctions. In
Proceedings of the 3rd ACM conference on Electronic
Commerce, pages 125–136, 2001

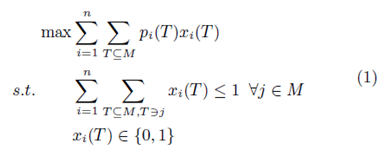
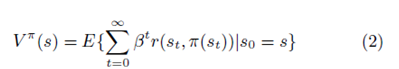







دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.