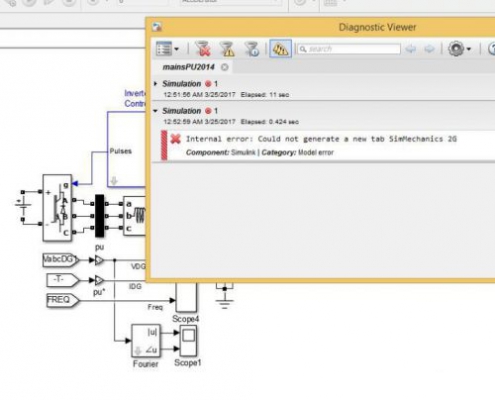
Internal error: could not generate a new tab SimMechanics 2G
/
0 نظرات
رفع مشکل Internal error: could not generate a new tab SimMech…

روش های مختلف shrinking و zooming
روش های بزرگنمایی با نوعی oversampling این کار را انجام می دهند. د…

راهکار ارائه پیشنهاد تطبیقی بر اساس یادگیری-Q در حراجهای ترکیبی
ترجمه مقاله:
A Q-Learning Based Adaptive Bidding Strategy i…
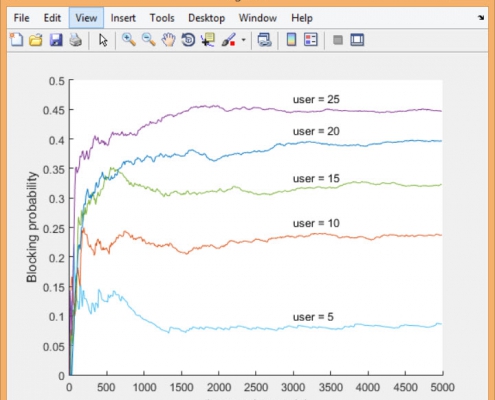
بدست آوردن تقریب سری تیلور مرتبه دوم با متلب
برای ییدا کردن تقریب سری تیلور مرتبه دوم, با یک مثال این کار را در…

آموزش مقدماتی Matlab – بخش هشتم
آموزش مقدماتی متلب در چند بخش تهیه شده و می توانید در ویلاگ مت…

آموزش مقدماتی Matlab – بخش هفتم
آموزش مقدماتی متلب در چند بخش تهیه شده و می توانید در ویلاگ مت…

آموزش مقدماتی Matlab – بخش ششم
آموزش مقدماتی متلب در چند بخش تهیه شده و می توانید در ویلاگ مت…

آموزش مقدماتی Matlab – بخش پنجم
آموزش مقدماتی متلب در چند بخش تهیه شده و می توانید در ویلاگ مت…

آموزش مقدماتی Matlab – بخش چهارم
آموزش مقدماتی متلب در چند بخش تهیه شده و می توانید در ویلاگ مت…
