توضیحات
طراحی سه بعدی مسیر بهینه ی پروازی مقید برای یک ربات پرنده ی چهارپره شش درجه آزادی جهت کاربردهای ترافیک شهری
Three-Dimensional Constrained Optimal Motion Planning for a Six-Degree of-Freedom Quadrotor Helicopter for Urban Traffic Purposes
شبیه سازی در محیط ام فایل متلب انجام شده است.
گزارش شامل 7صفحه در قالب ورد است.
در شبیه سازی مقاله به موراد زیر توجه شده:
طراحی بهینه مسیر کوادروتور که بلند شده، مسیری مشخص را طی کند، پس از تحویل بسته برگردد. تابع هدف حداقل تلاش کنترلی است. در راه تعدادی مانع ثابت موجود است. از روش تبدیل مسئله کنترل بهینه به برنامه ریزی غیرخطی حل شود.
تا حدودی مانند مقاله, اما با چند تفاوت:
1. مسئله حداقل تلاش کنترلی
2. مسیر رفت و برگشت
3. موانع بهتر از مقاله
چکیده
ترافیک، یک واژه ی شناخته شده ی بین المللی است که یکی از مهمترین عوامل ایجاد آن در کشورهای توسعه یافته افزایش جمعیت میباشد.
بررسی ها نشان میدهد که بهترین راه کنترل ترافیک و به مفهوم دیگر به حداقل رساندن ضرر و زیان ناشی از آن، استفاده از عواملی است که گزارشات ترافیک را در بهینه ترین زمان ممکن انجام دهد.
لذا در این پژوهش به منظور کنترل ترافیک، پس از مدلسازی ربات پرنده ی چهارپره توسط رابطه ی نیوتن اویلر، یک مسیر سه بعدی بهینه ی مقید با استفاده از تکنیک ترتیب مستقیم طراحی شده است.
به عبارت دیگر، ابتدا مسئله ی مطرح شده در این پژوهش به عنوان یک مسئلۀ کنترل بهینه فرموله شده است و سپس مسئله ی کنترل بهینه با استفاده از رویکرد ترتیب مستقیم که یکی از روش های حل عددی مسائل کنترل بهینه است، کاملا گسسته شده و به یک مسئلۀ برنامه ریزی غیرخطی 1 تبدیل گردیده است .
در نهایت حل مسئله ی برنامه ریزی غیرخطی فوق الذکر از طریق حل کننده ی SNOPT صورت گرفته است که برای حل از روش های گرادیانی نظیر SQP بهره می گیرد.
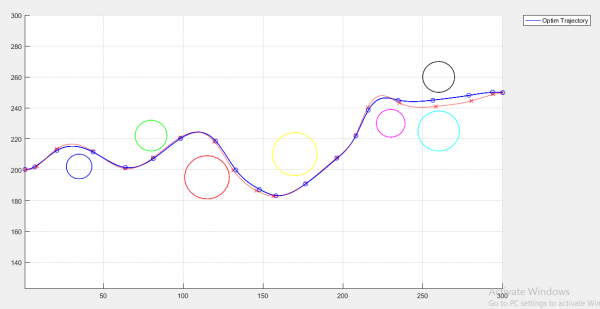
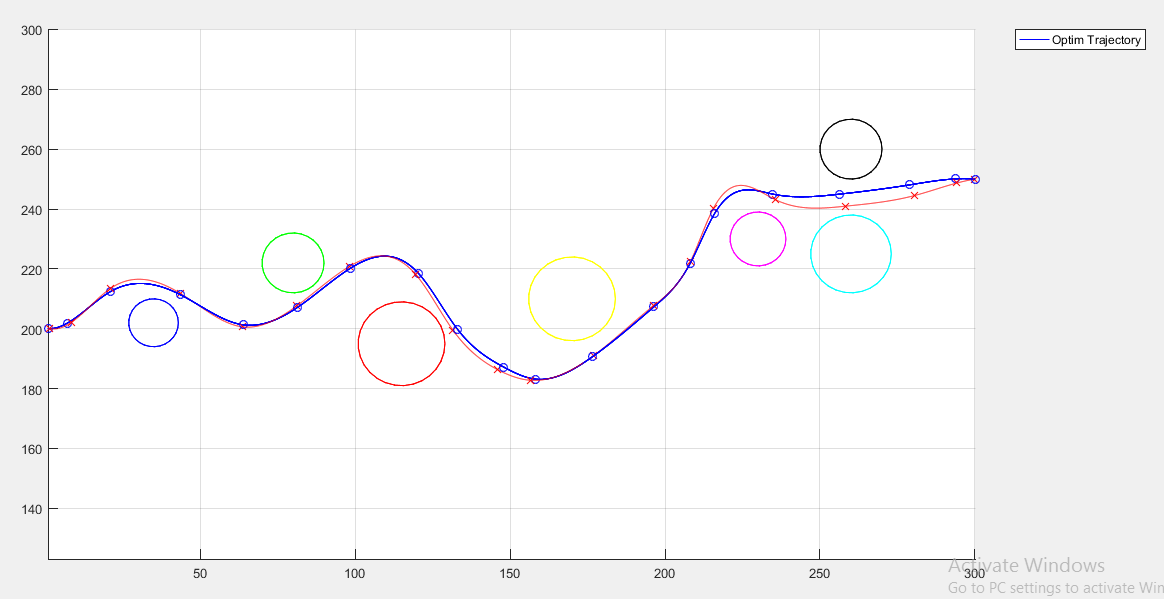
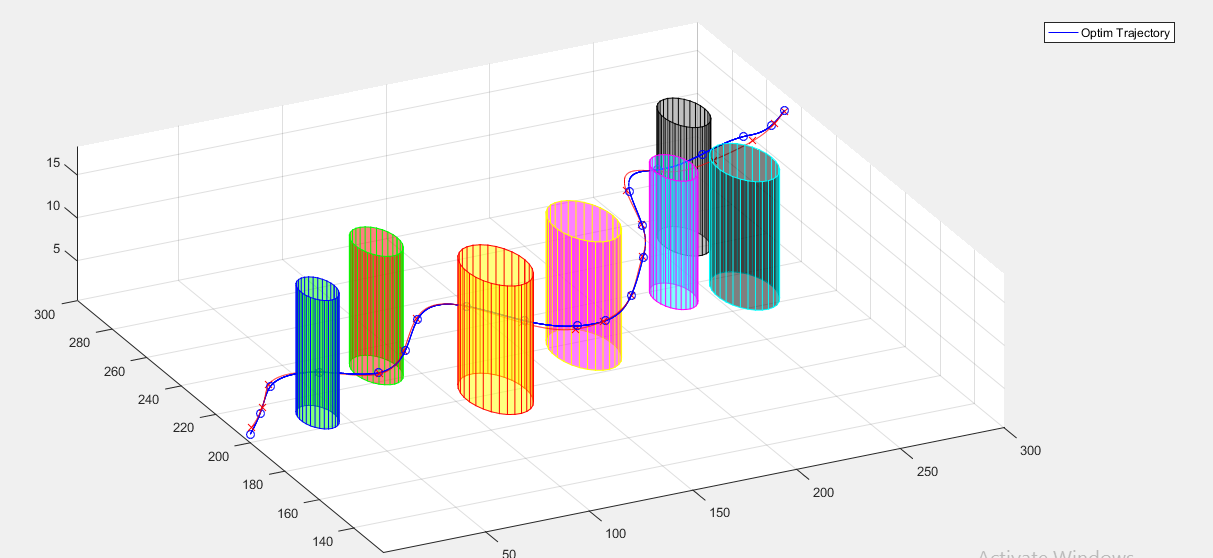
لازم به ذکر است از آن جایی که هدف غایی طراحی مسیر در این پژوهش، کنترل ترافیک شهری میباشد، لذا قیدهای در حین مسیر تعریف شده در حل این مسئله از نوع قیدهای شهری هستند بدین صورت که هر ساختمان در مسیر پروازی با یک استوانه مدل شده است.
نتایج حاصل از شبیه سازی نشان میدهند که روش فوق الذکر، یک روش کارامد و موثر در طراحی سه بعدی مسیر بهینه ی پروازی میباشد.
بخشی از گزارش شبیه سازی
مقدمه:
در این گزارش به پیاده سازی و ارتقاء مقاله مذکور در طراحی مسیر بهینه کوادراتور با شش درجه آزادی می پردازیم.
در این مقاله با استفاده از روش های بهینه سازی عددی برای مدل های مقیاس بزرگ، سعی در طراحی یک مسیر بهینه برای کوادراتور شده است، به نحوی که به موانع موجود در سر راه برخورد نکند و همچنین زمان حرکت را کمینه کند.
در این گزارش اما مسیر به صورت رفت و برگشت طراحی شده است، زمان حرکت مشخص فرض شده و سعی در کمینه کردن تلاش کنترلی شده است و از طرفی نیز موانع بیشتری در نظر گرفته شده است.
در مقاله مورد نظر از تولباکس SNOPT جهت بهینه سازی مسیر به زبان فرترن استفاده شده است، ولیکن در این گزارش با توجه به پولی بودن تولباکس SNOPT در متلب از تولباکس OPTI و روش بهینه سازی IPOPT استفاده شده است.
لازم به ذکر است از آنجا که در این گزارش قصدی مبنی بر بهینه کردن زمان نداشتیم لذا عملا روابط 37 در مقاله نیازی به استفاده کردن نداشتند.
به طور کلی در این مقاله بعد از استخراج روابط دینامیکی حاکم بر کوادراتور که در روابط 26 و 27 بیان شده است، برای بهینه سازی مسیر از روش ترتیب مستقیم استفاده شده است.
لازم به ذکر است که در این روش مسیر به صورت پیوسته طراحی نمی شود، بلکه ابتدا مسیر را به چند قسمت تبدیل می کنیم و سعی می کنیم که جایگاه این نقاط را در طول مسیر به نحوی پیدا کنیم که مسیر گذرنده از آن پیوسته باشد.
در این گزارش برای مسیر رفت، 20 گره و برای مسیر برگشت نیز 20 گره استفاده شده است.
در ادامه معادلات پیوسته با استفاده از تقریب های عددی باید به صورت گسسته نوشته شوند که بدین منظور از روش گفته شده در رابطه 31 استفاده شده است. این رابطه به صورت 32 بازنویسی شده و در طول بهینه سازی سعی می شود که مقدار صفر شود، که بعنوان یکی از قیود مساوی تعریف می شود.
همچنین در طول بهینه سازی سعی می شود که فاصله گره های مدنظر در فاصله ای بیشتر از شعاع موانع و یک ضریب اطمینان برای طراحی در نظر کرفته شود که در این طراحی این ضریب اطمینان 1.2 در نظر گرفته شده است. یعنی برای یک مانع با شعاع 10 متر باید در طول بهینه سازی مسیر فاصله گره ها از مرکز مانع کمتر از 11 نشود. که این نیز به صورت یک قید نامساوی در نظر گرفته شده است.
بررسی کد متلب
برای اجرای کد کافی است فایل main_IPOPT.m که ضمیمه شده است را اجرا کنید. در این کد ابتدا پارامترهای مورد نیاز شبیه سازی تعریف می شوند. در ادامه موانع به تعداد 7 عدد تعریف می شوند. که شامل مرکز، و شعاع آن ها می باشد و مقادیر مورد نیاز برای رسم آن ها!
بخشی از گزارش , شامل کدهای متلب و توضیح آن در اینجا نیامده است.
در ادامه حل بهینه در متغیر x_Opt قرار می گیرد. با استفاده از تابع زیر مقادیر طراحی شده برای مسیر بهینه را به صورت منظم و به دو قسمت مسیر رفت و برگشت تقسیم می کنیم.
%% Get info of Trajectory
Opt_Traj = getSmoothTraj(x_Opt);
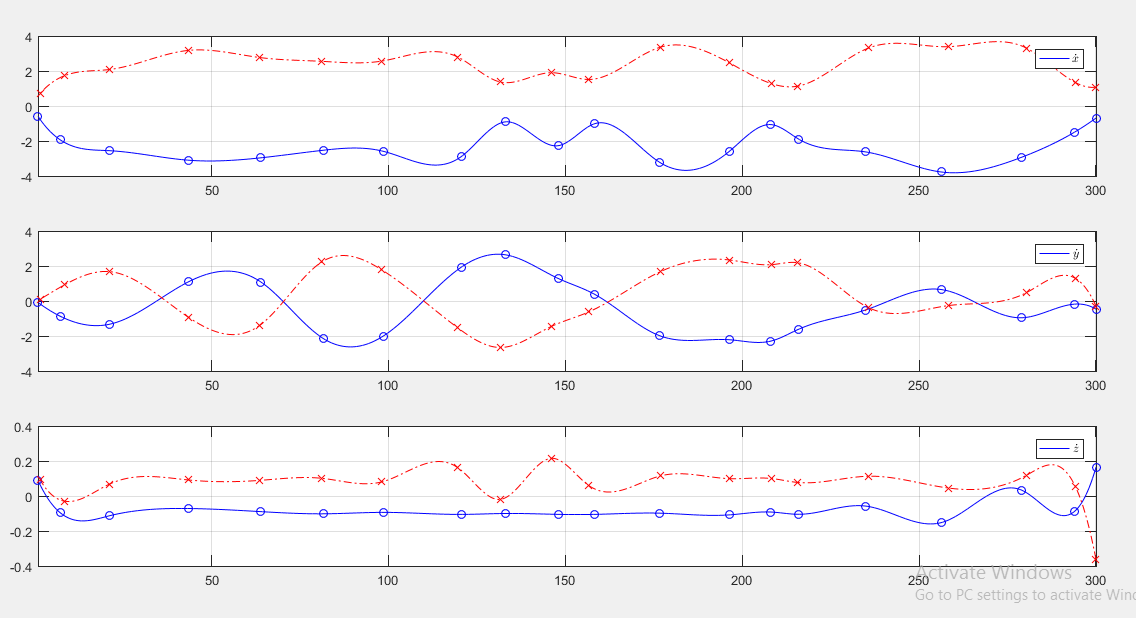
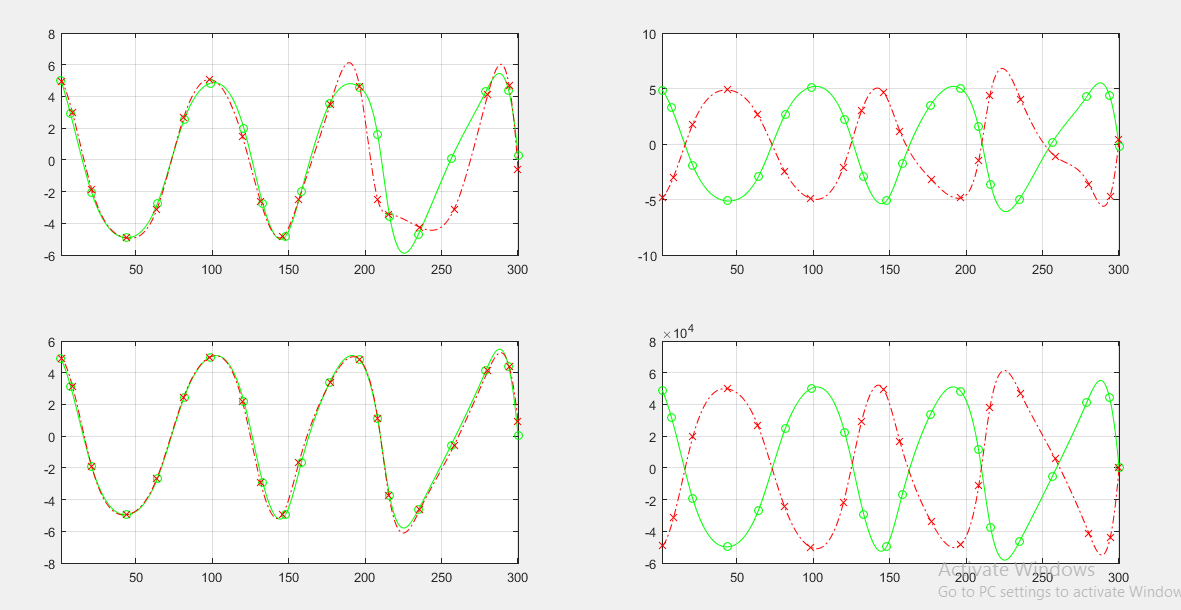
تمام اطلاعات مسیر در متغیر Opt_Traj ذخیره شده است. در ادامه به رسم این مقادیر بر حسب مکان (مشابه مقاله) می پردازیم. و خروجی آن به صورت زیر است!
نتایج فوق برای تعداد تکرار 10 در بهینه سازی بدست آمده است.
از آن جا که برای حدس اولیه مقادیر مسیر از روش جایگذاری عددی استفاده شده است، و بستگی به جایگاه موانع و دیگر مشخصه های مسیر دارد، لذا قابل ملاحظه در آن ها ممکن است باعث ناپداری در بهینه سازی شود.
لذا جهت تغییرات در مسیر پروازی حتما باید متناسب با آن حدس اولیه Xinit نیز تغییرات لازم را داشته باشد.
حدس اولیه در مقاله نیست و نویسنده نیز پاسخی نداد و مجری حدس اولیه را بر اساس خطا و آزمون در نظر گرفته است.
توضیحات برنامه نویس:
باید تعداد تکرارها رو زیاد بگیرید که به صورت کاملا درستی بهینه سازی اتفاق بیافته، من چون سیستمی که دارم کند هست نتوانستم برای مثلا 2000 تا تکرار خروجی بگیرم. ولی این مسئله حدود 1050 تا قید دارد و در حدود 640 متغیر بهینه سازی که همین باعث میشود که کار بهینه سازی بسیار سخت و طولانی شود.
متاسفانه مقاله اصلی و مقاله بهبود یافته هم چیزی در مورد ماتریس ژاکوبین مسئله نگفتند که بشود کمک کرد به حل سریع تر مسئله! و از طرفی هم solver مقاله snopt هستش که پولی هست واسه متلب و رایگان نیست و فکر کنم solver قوی تری هست نسبت به ipopt که استفاده کردیم.
کلیدواژه:
ربات پرنده چهارپره, مسیر سه بعدی بهینه ی مقید, رویکرد ترتیب مستقیم, ترافیک شهری
Quadrotor Helicopter, Three Dimensional Motion Planning, Direct Collocation Approach, Urban Traffic
شبیه سازی
طراحی سه بعدی مسیر بهینه ی پروازی مقید برای یک ربات پرنده ی چهارپره شش درجه آزادی جهت کاربردهای ترافیک شهری
توسط کارشناسان سایت متلبی تهیه شده است و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،.
با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.



نقد و بررسیها
هنوز بررسیای ثبت نشده است.