توضیحات
MIMO adaptive fuzzy terminal sliding-mode controller for robotic manipulators
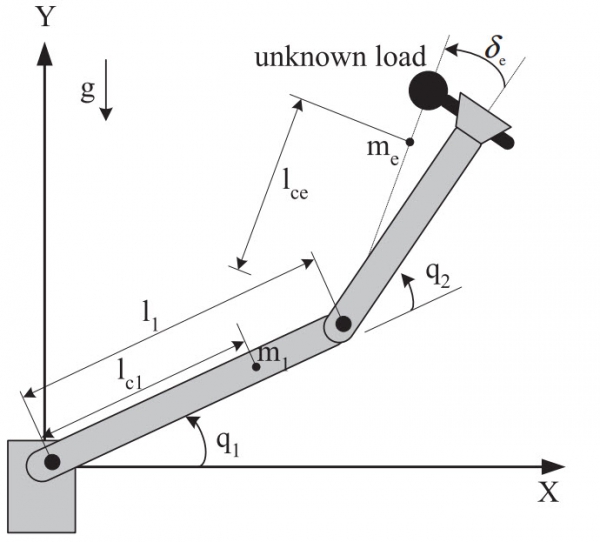
در این مقاله کنترل فازی تطبیقی مود لغزشی برای یک بازوی ربات دو لینکی در نظر گرفته شده است. دینامیک ربات به صورت زیر میباشد
هدف تنظیم بردار موقعیت q در مقدار دلخواه و مطلوب است، بردار خطای ردیابی e را به صورت زیر تعریف میکنیم
برای طراحی کنترل کننده مودلغزشی ابتدا باید یک سطح لغزش برای سیستم کنترل طراحی شود، در این مقاله از دو سطح لغزش استفاده شده است. یک سطح لغزش خطی و دیگری غیرخطی است. در کنترل سیستم با سطح لغزش غیرخطی همگرایی در یمان محدود اتفاق میافتد در حالی که در کنترل با سطح لغزش خطی، همگرایی به صورت مجانبی میباشد.
سطح لغزش غیرخطی به صورت زیر تعریف شده است
که در آن داریم
و که تمامی پارامترها اکیدا مثبت هستند.
همچنین سطح لغزش خطی به صورت زیر تعریف میشود
که در آن که تمامی پارامترها اکیدا مثبت هستند.
اگر سطح لغزش غیرخطی را در نظر بگیریم، میتوان سطح لغزش و مشتق آن را به صورت زیر بازنویسی کرد
که در آن
با جایگذاری سطح لغزش و مشتق آن در معادلات دینامیک سیستم، خواهیم داشت
حال برای اثبات پایداری سیستم، و طراحی کنترل کننده به نحوی که تضمین پایداری داشته باشیم، یک تابع کاندید لیاپانوف به صورت زیر پیشنهاد میدهیم
با مشتق گیری از معادله فوق، و جایگذاری از (14) خواهیم داشت
اگر قانون کنترل را به صورت زیر پیشنهاد دهیم
که در آن یک ماتریس قطری با المانهای اکیدا مثبت است، در نتیجه مشتق تابع لیاپانوف به صورت زیر بدست میآید
که در آن
که اگر K به اندازه کافی بزرگ انتخاب شود، پایداری سیستم تضمین میشود، ولی این کنترل کننده حالت سوئیچینگ داشته و یک کنترل کننده بهره بالا میشود که خود معایب دیگری در سیستم ایجاد میکند.
در این مقاله برای تضمین پایداری، و کنترل سیستم، از قانون کنترل زیر استفاده کرده است، در واقع در قانون کنترل زیر خروجی کنترل کننده است، u بخش کنترل فازی تطبیقی، s سطح لغزش و بهره تطبیق است. یعنی قانون کنترل شامل دو جمله مجزا است، که یکی فازی تطبیقی و دیگری تطبیقی است.
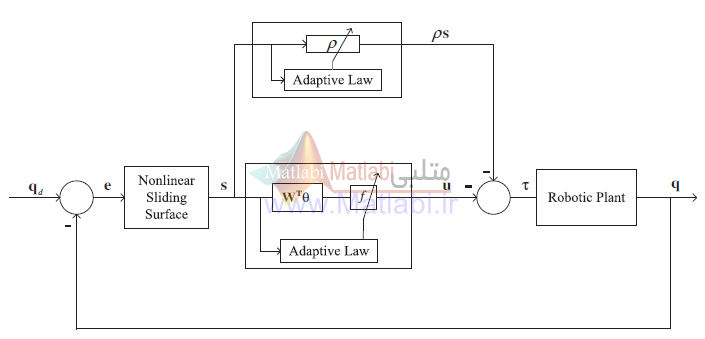
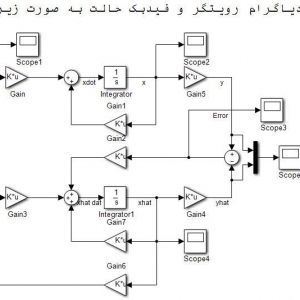
با توجه به مطالب فوق، میتوان نمودار بلوکی سیستم حلقه بسته را به صورت زیر در نظر گرفت
مشاهده میشود که مقدار مطلوب qd است که موقعیت دو joint یا مفصل بازو است که به سیستم داده میشود، با q که مقدار واقعی است (و اندازه گیری میشود) مقایسه شده و خطای ردیابی e تولید میشود، این خطا به بلوک nonlinear sliding surface می رود که در این بلوک سطح لغزش غیرخطی ساخته میشود، سطح لغزش ورودی کنترل کننده است، در شکل بالا نیز دیده میشود که کنترل کننده شامل دو بخش است، یک بخش فازی تطبیقی و یک بخش دیگر بخش تطبیقی میباشد، حاصل جمع این دو خروجی کنترل کننده را تولید کرده و به فرایند (ربات ) داده میشود.
حال هر بخش از کنترل کننده را به صورت جداگانه شرح میدهیم
همانطور که در بخش قبل گفته شده، برای تضمین پایداری باید مشتق تابع کاندید لیاپانوف که به صورت زیر است منفی شود تا پایداری سیستم تضمین گردد
در معادله فوق Bi یک تابع غیرخطی از دینامیکهای سیستم است و هدف طراحی ui برای بدست آوردن یک کنترل پایدار است.
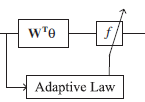
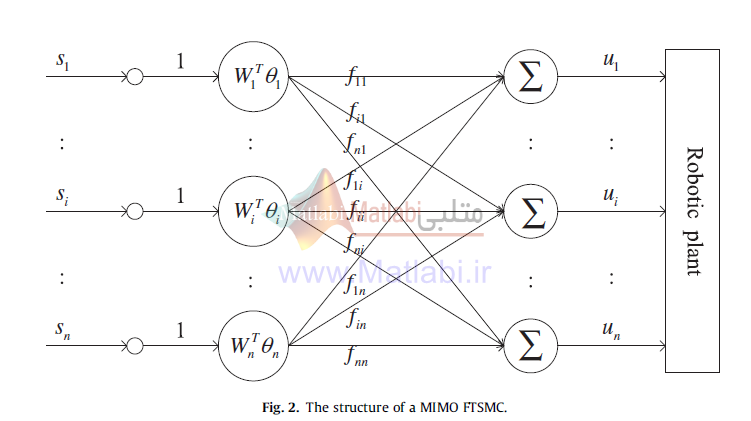
ما ابتدا بخش کنترل فازی تطبیقی را طراحی میکنیم، بخش فازی تطبیقی شامل یک سیستم فازی ثابت و یک بهره تطبیقی که در خروجی سیستم فازی ضرب میشود است. یعنی یک سیستم فازی ثابت داریم، که خروجی آن در یک بهره تطبیقی ضرب میشود. ساختار این سیستم به صورت زیر است
در شکل فوق فرمول سیستم فازی و f بهره تطبیقی خورجی است که در خروجی سیستم فازی ضرب میشود. قانون تطبیق وظیفه، تطبیق f را دارد. سیستم فازی ثابت بوده و شامل 5 قانون اگر-آنگاه زیر است
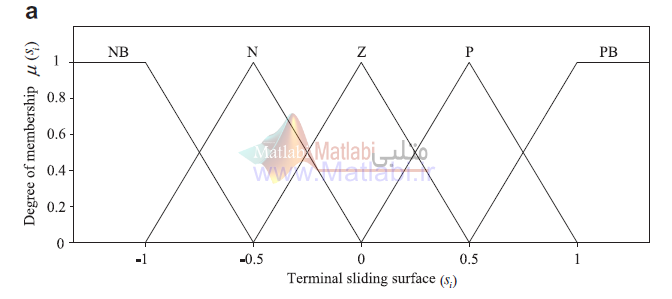
این قوانین فازی ثابت بوده و تغییر نمیکنند، توابع تعلق ورودی و خروجی مجموعه قوانین فازی فوق به صورت زیر میباشند
توابع تعلق ورودی
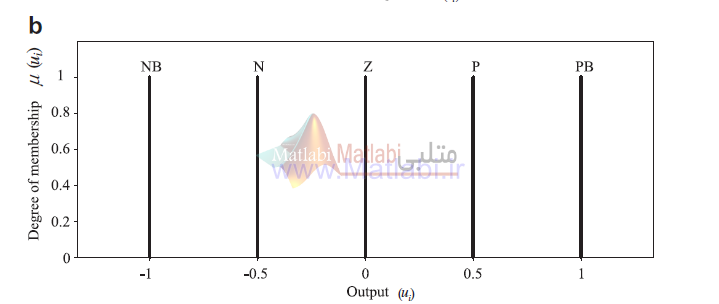
توابع تعلق خروجی
میدانیم که هر سیستم فازی به شکل فوق که شامل قوانین اگر-آنگاه است، را میتوان به صورت یک فرمول ریاضی به صورت زیر نوشت
که در آن بردار پارامترهای قسمت آنگاه از قوانین است (توابع تعلق خروجی) و ها نیز مربوط به قسمت اگر از قوانین فازی (توابع تعلق ورودی فازی) هستند. این سیستم فازی را به صورت برداری میتوان به شکل زیر بازنویسی کرد
که در آن
درواقع چون سیستم چند ورودی چند خروجی است، سیستم فازی به صورت برداری بدست میآید (یعنی کلن قانون کنترلی نیز برداری است چون سیستم چند ورودی چند خروجی میباشد) پس n سیستم فازی داریم، تمامی سیستم های فازی ثابت هستند و خروجی آنها در یک بهره ضرب میشوند که این بهره به صورت تطبیقی بدست آمده است. میتوان هر سیستم فازی را به صورت زیر نوشت
که در آن fi بهره خروجی مربوط به سیستم فازی iام و uic سیستم فازی iام است. قانون کنترل فوق در مقاله به عنوان قانون کنترل فازی تطبیقی تک ورودی تک خروجی یا siso AFTSMC گفته میشود.
یک حالت دیگر در طراحی سیستم کنترل فازی این است که برای خروجی iام از کنترل کننده به جای اینکه فقط از سیستم فازی iام استفاده کنیم از ترکیب تمامی سیستم های فازی استفاده کنیم، یعنی شکل زیر
ی
به این ساختار در مقاله کنترل فازی تطبیقی چند متغیره گفته شده یا MIMO AFTSMC. یعنی خروجی i ام کنترل کننده شامل ترکیب تمامی سیستم های فازی است. قانون کنترل در این حالت به صورت زیر نوشته میشود
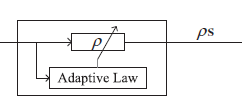
تا این قسمت کنترل کننده برای سیستم طراحی شد، اما در مقاله گفته شده برای بهبود عملکرد سیستم و افزاییش مقاوم بودن آن یک جمله تطبیقی جدید به قانون کنترل فازی چه حالت siso و چه حالت mimo اضافه میکنیم، این قانون کنترل به صورت زیر است
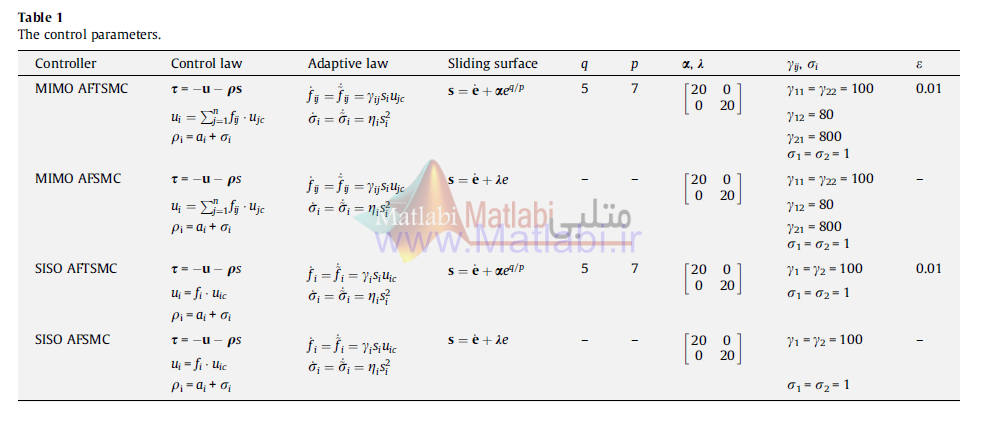
که در آن s سطح لغزش است. قوانین تطبیق و پارامترهای کنترل کننده در جدول زیر در مقاله داده شده است
4 قانون کنترل مختلف در جدول دیده میشود، در حالت MIMOدو قانون کنترل داریم یکی حالت فازی تطبیقی mimo است که برای دو حالت سطح لغزش خطی و غیرخطی طراحی شده، و در حالت siso نیز دو حالت مختلف داریم که یکی برای سطح لغزش خطی و دیگری برای سطح لغزش غیرخطی است. قوانین تطبیق برای سیستم کنترل فازی تطبیقی در جدول بالا برای هر 4 قانون کنترل به نحوی بدست آمده است که تضمین پایداری داشته باشیم.
برای تضمین پایداری تابع کاندید لیاپانوف به صورت زیر پیشنهاد میشود
که با مشتق گیری و ساده سازی قوانین تطبیق از آن بدست میآیند.
4 قانون کنترل مختلف داریم، که در مقاله دو مثال شبیه سازی داده شده است، یعنی 16 شبیه سازی مختلف است.
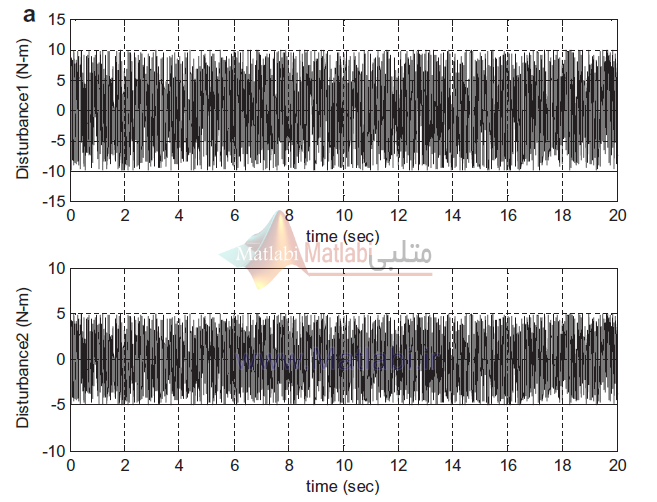
برای تمام شبیه سازی ها، اغتشاش در مقاله به صورت زیر داده شده است(برای هر دو لینک)
که ما این دو اغتشاش را به صورت زیر در تمامی شبیه سازی ها شبیه سازی کردیم
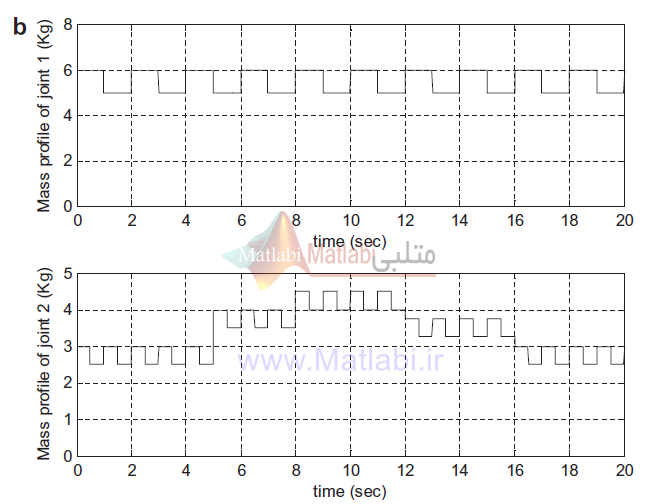
همچنین عدم قطعیت پارامتری در مقاله در نظر گرفته شده و جرم دو لینک از ربات متغیر با زمان است، و به صورت زیر تغییر میکند
که ما این دو تغییر جرم و عدم قطعیت را در تمامی شبیه سازی ها به صورت زیر مدل سازی و شبیه سازی کردیم
شبیه سازی برای دو حالت مختلف در نظر گرفته شده است.
در مثال 1 که شبیه سازی های مربوط به آن در پوشه EX1 است، ورودی مرجع سینوسی میباشد
و در مثال 2 که شبیه سازی های مربوط به آن در پوشه EX2 است ورودی مرجه به صورت پله ای است.
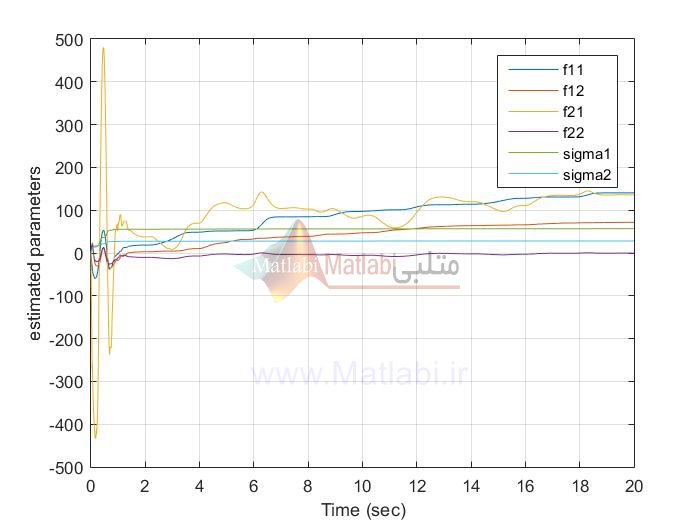
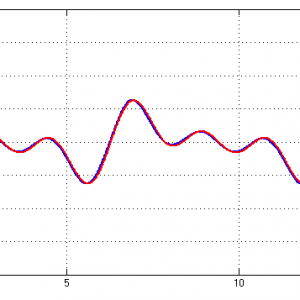
نتایج شبیه سازی با متلب پوشه EX1:
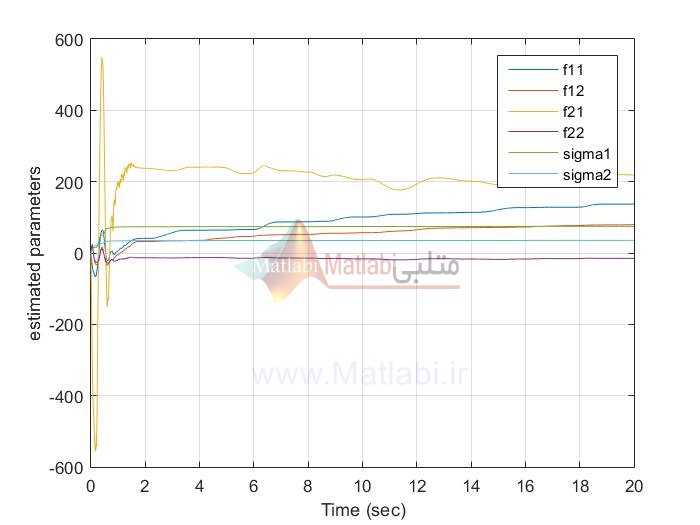
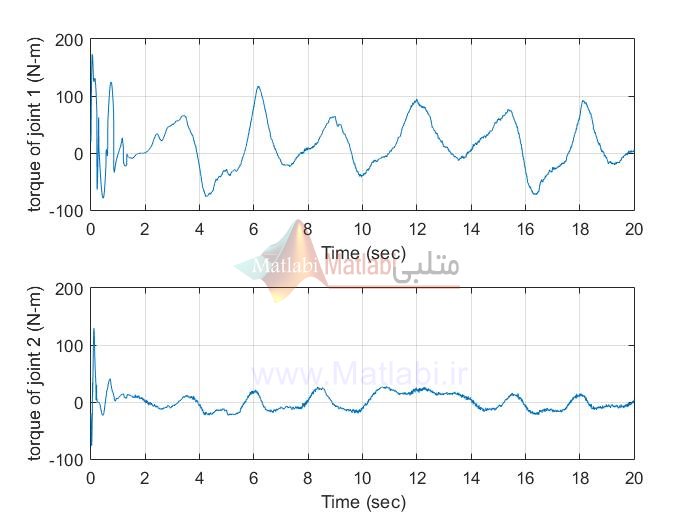
MIMO_AFSMC
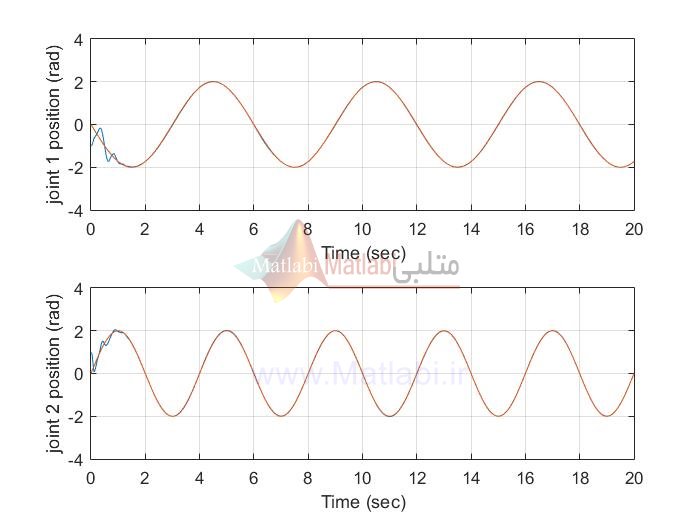
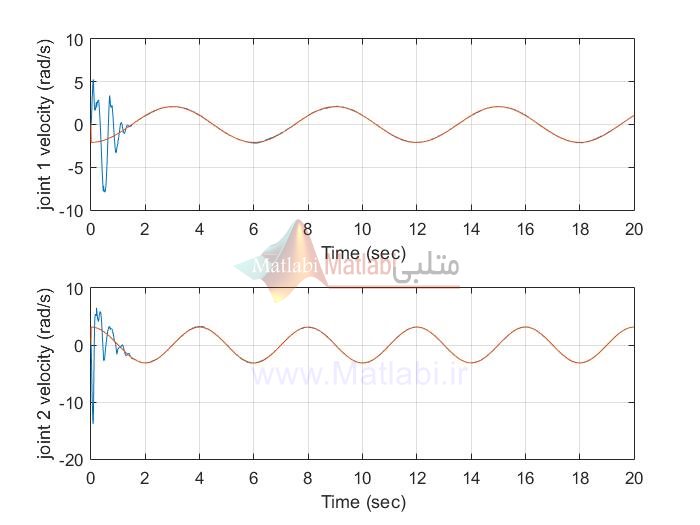
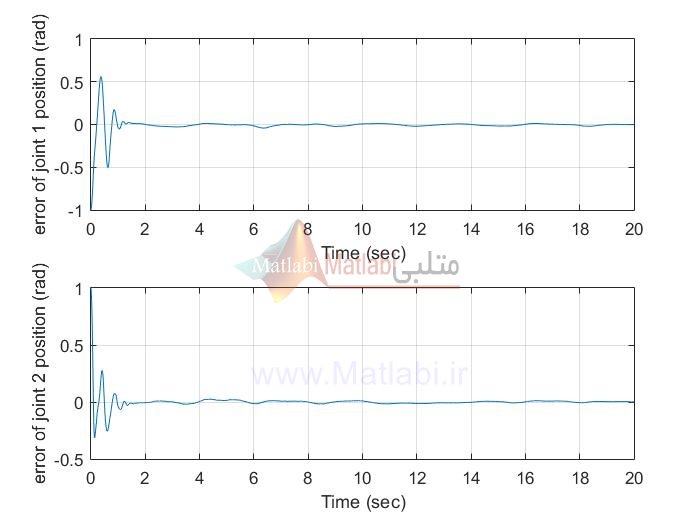
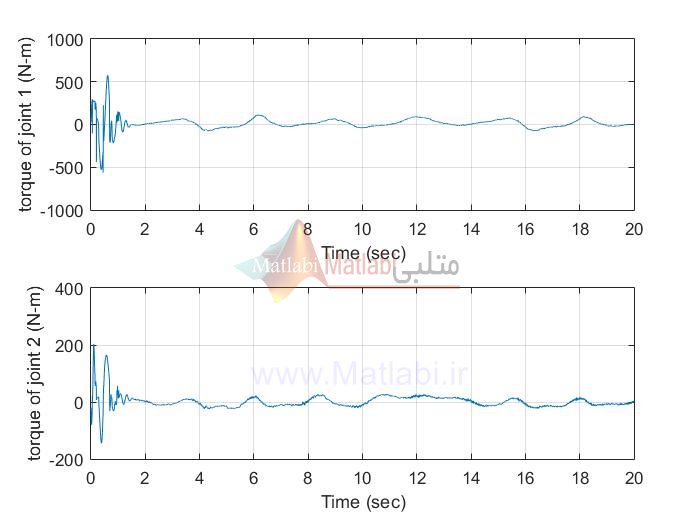
MIMO AFTSMC
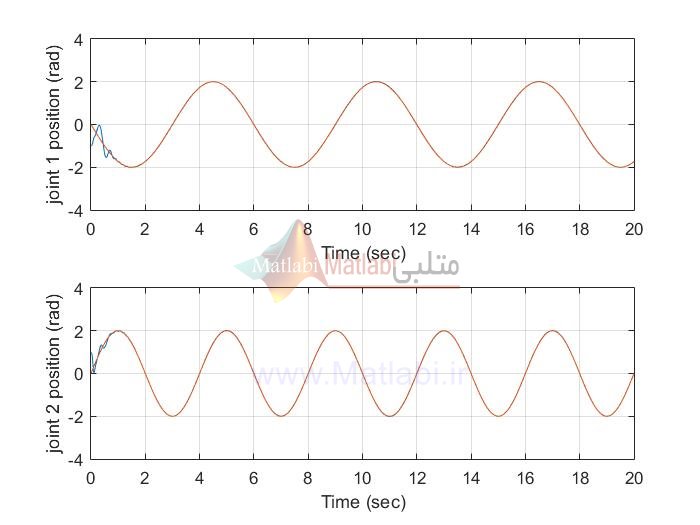
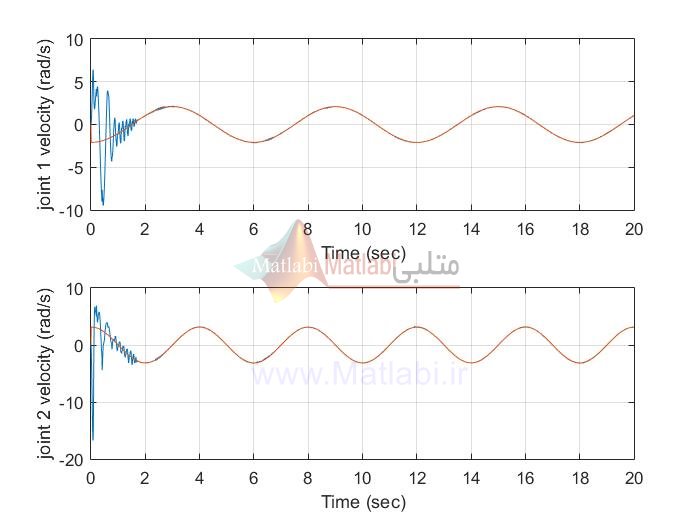
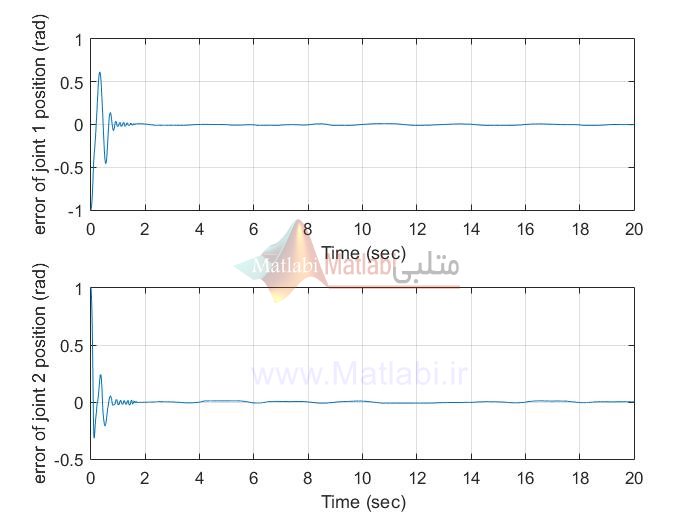
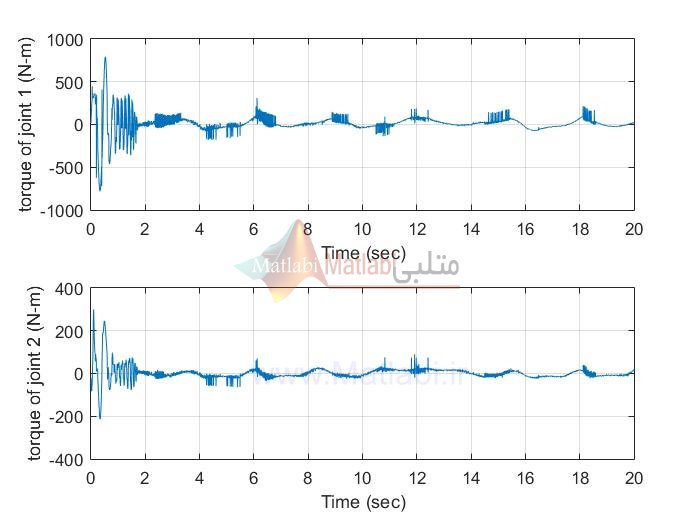
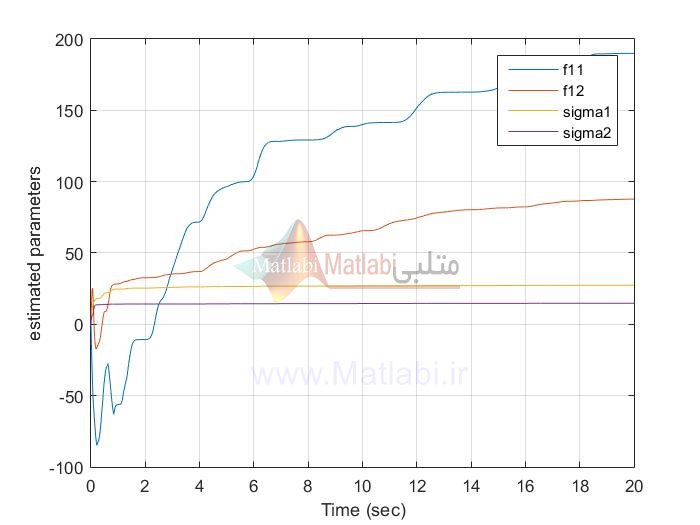
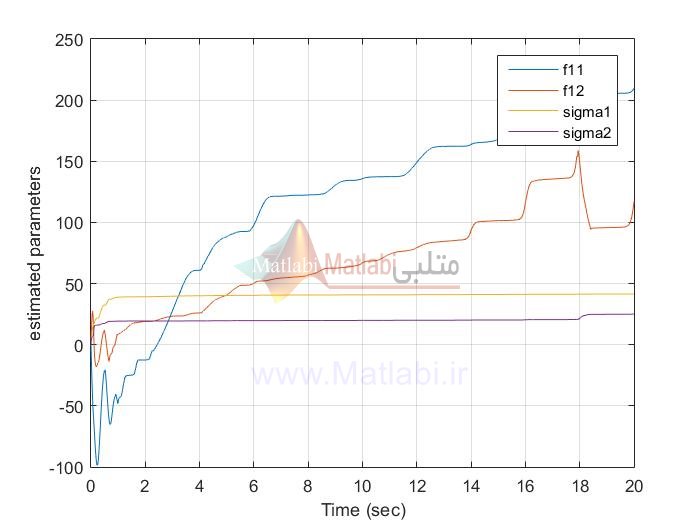
siso AFSMC
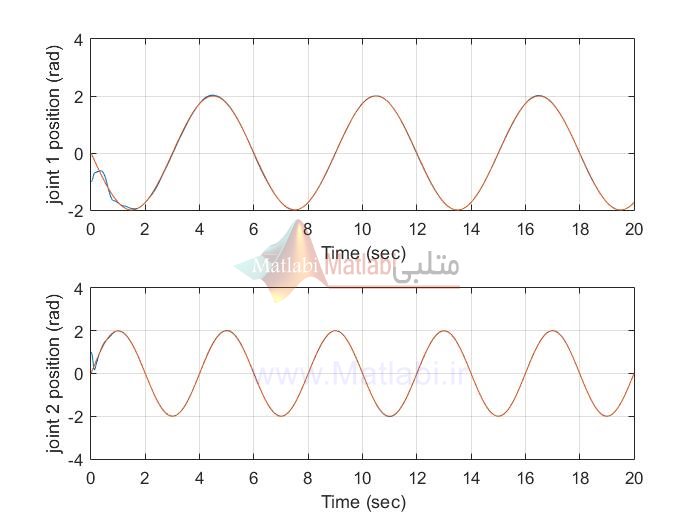
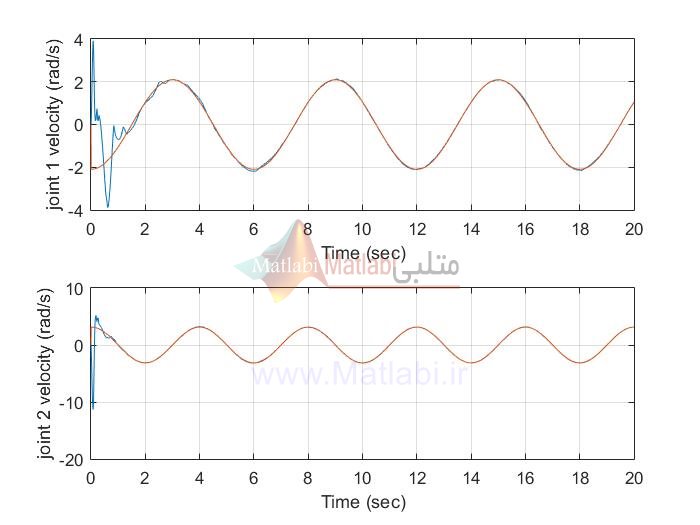
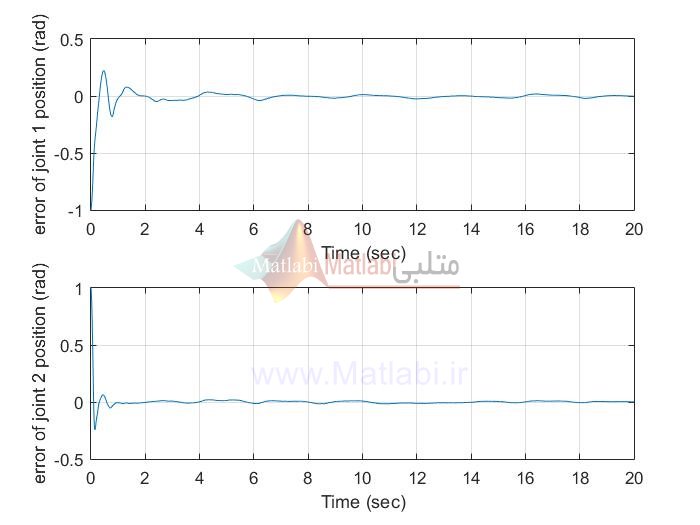
siso AFTSMC
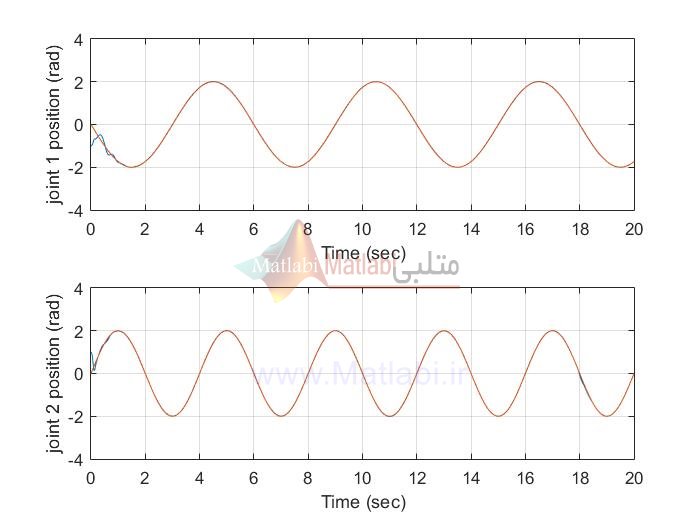
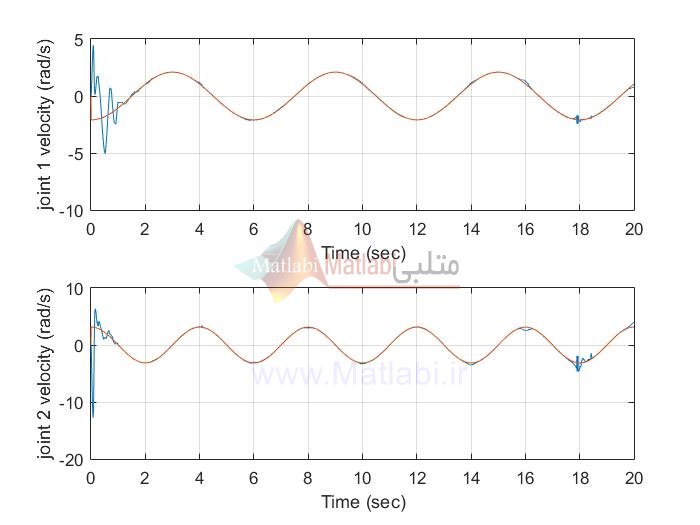
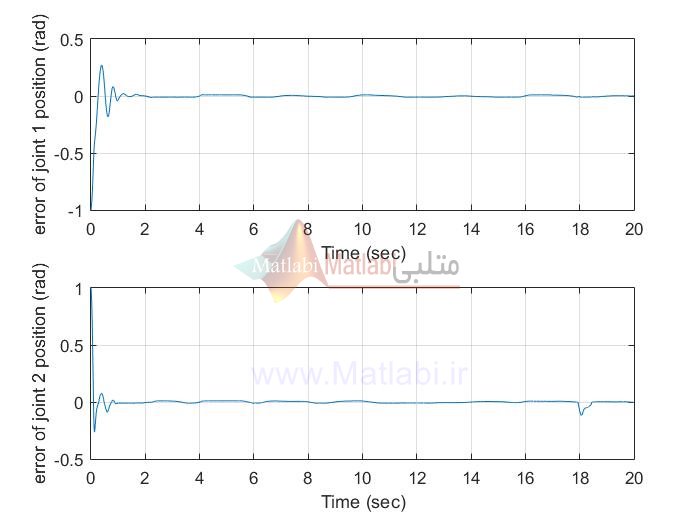
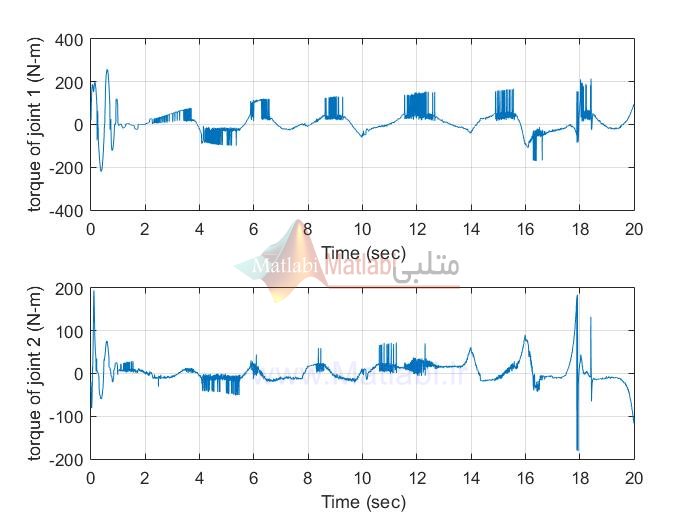
نتایج شبیه سازی با متلب پوشه EX2 بدلیل طولانی شدن در اینجا قرار داده نشده است. با خرید پروژه تمامی نتایج را با اجرای برنامه متلب می توان دید.
کلید واژه :
Adaptive control, Fuzzy logic controller, Robotic manipulators, Sliding-mode, پروژه متلب Terminal sliding-mode
- کنترلر مود لغزشی پایانه فازی تطبیقی MIMO برای دستکاری کننده های رباتیک
شبیه سازی مقاله MIMO adaptive fuzzy terminal sliding-mode controller for robotic manipulators
توسط کارشناسان سایت متلبی پیاده سازی گردیده و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.

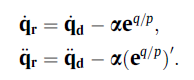
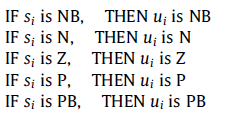
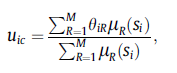
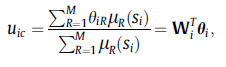
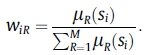
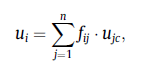
نقد و بررسیها
هنوز بررسیای ثبت نشده است.