حداقل مربعات در متلب
حداقل مربعات در متلب را با چند مثال مختلف بررسی می کنیم.
برای آموزش شبیه سازی روش های حداقل مربعات و حداقل مربعات بازگشتی و… در متلب مثال های عملی را با هم بررسی می کنیم.
فرض کنیم چنین سوالاتی مطرح است:
1-سیستم زیر را در نظر بگیرید که در آن ) e(tنویز سفید با واریانس 0/1است.
![]()
فرض کنید پارامتر a=0.7و b=2باشد با اعمال روش هاي
الف- حداقل مربعات و ب- حداقل مربعات بازگشتی تخمین پارامترهاي aو bرا بدست آورید و رسم نمایید.تغییرات پارامترها
را نسبت به تعداد تکرارها رسم نموده و نحوه همگرایی تخمین پارامترها را توضیح دهید.سپس روشهاي مختلف را با هم
مقایسه کنید.
-2فرض کنید مدل ریاضی سیستم بصورت زیر است
![]()
ورودي uبه سیستم و خروجی yبه صورت زیر است پارامترهاي a0و b0و b1را با روش حداقل مربعات تخمین بزنید.

-3سیستم
![]()
با ورودي PRBSکه داراي دامنه ±1است در نظر بگیرید با فرض ) e(tنویز سفید با واریانس واحد شبیه سازي کنیددو
مدل براي سیستم زیر در نظر بگیرید
با در نظر گرفتن N=100این مدلها را با روش هاي
حداقل مربعات
حداقل مربعات تعمیم داده شده
متغییرهاي کمکی
تخمین زده و با هم مقایسه کنید
با پروژه آماده متلب که در زیر قرار داده شده و آموزش آن با کامنت گذاری مشخص شده است بخوبی میتوان همه مراحل را دید:
=================================
clc;پاک کردن صفحه متلب
clear all;پاک کردن متغیرهای گذشته و بلا استفاده
close all;بستن نمودارهای باز
%==========================================================================
%Q1سوال شماره 1
a=0.7;مقدار پارامتر
b=2;مقدار پارامتر
sigm_e=0.1;واریانس نویز
N=100;تعداد داده ها
N1=N;متغیر کمکی برای ذخیره تعداد داده ها
y=zeros(1,N);تعریف بردار خروجی
u=50*idinput(N);ورودی شناسایی
ep=wgn(1,N,0);نویز سفید
sigm_ep=1/(N)*sum(ep.^2);واریانس نویز
e=sqrt(sigm_e/(sigm_ep))*ep;ایجاد نویز با واریانس مورد نظر
جمع آوری داده از سیستم
for t=2:N
y(t)=-a*y(t-1)+b*u(t-1)+e(t);
end
y1=y;u1=u;
ترسیم داده های شناسایی
figure (1)
subplot(2,1,1);stairs(1:1:N,y,’b’,’linewidth’,2);grid on;axis([1 N -400 400]);ylabel(‘y’);
subplot(2,1,2);stairs(1:1:N,u,’b’,’linewidth’,2);grid on;axis([1 N -60 60]);ylabel(‘u’);xlabel(‘sample’);
%Least squaresروش حداقل مربعات
Phi=zeros(N-1,2);ماتریس داده ها
Y=zeros(N-1,1);بردار خروجی
for t=2:N
Phi(t,:)=[-y(t-1),u(t-1)];
Y(t)=y(t);
end
teta=(Phi.’*Phi)\Phi.’*Y;محاسبه پارامترها
teta1=teta;
نمایش مقادیر داده در صفحه متلب
disp(‘Q1: Least squares estimation for N=100’);
disp(‘estimated a=’);disp(teta(1));
disp(‘estimated b=’);disp(teta(2));
N=200;تکرار شبیه سازی برای تعداد داده های بیشتر
N2=N;
y=zeros(1,N);
u=50*idinput(N);
ep=wgn(1,N,0);
sigm_ep=1/(N)*sum(ep.^2);
e=sqrt(sigm_e/(sigm_ep))*ep;
for t=2:N
y(t)=-a*y(t-1)+b*u(t-1)+e(t);
end
y2=y;u2=u;
Phi=zeros(N-1,2);
Y=zeros(N-1,1);
for t=2:N
Phi(t,:)=[-y(t-1),u(t-1)];
Y(t)=y(t);
end
teta=(Phi.’*Phi)\Phi.’*Y;
teta2=teta;
disp(‘Q1: Least squares estimation for N=200’);
disp(‘estimated a=’);disp(teta(1));
disp(‘estimated b=’);disp(teta(2));
N=300;تکرار شبیه سازی برای تعداد داده های بیشتر
N3=N;
y=zeros(1,N);
u=50*idinput(N);
ep=wgn(1,N,0);
sigm_ep=1/(N)*sum(ep.^2);
e=sqrt(sigm_e/(sigm_ep))*ep;
for t=2:N
y(t)=-a*y(t-1)+b*u(t-1)+e(t);
end
y3=y;u3=u;
Phi=zeros(N-1,2);
Y=zeros(N-1,1);
for t=2:N
Phi(t,:)=[-y(t-1),u(t-1)];
Y(t)=y(t);
end
teta=(Phi.’*Phi)\Phi.’*Y;
teta3=teta;
disp(‘Q1: Least squares estimation for N=300’);
disp(‘estimated a=’);disp(teta(1));
disp(‘estimated b=’);disp(teta(2));
N=400;تکرار شبیه سازی برای تعداد داده های بیشتر
N4=N;
y=zeros(1,N);
u=50*idinput(N);
ep=wgn(1,N,0);
sigm_ep=1/(N)*sum(ep.^2);
e=sqrt(sigm_e/(sigm_ep))*ep;
for t=2:N
y(t)=-a*y(t-1)+b*u(t-1)+e(t);
end
y4=y;u4=u;
Phi=zeros(N-1,2);
Y=zeros(N-1,1);
for t=2:N
Phi(t,:)=[-y(t-1),u(t-1)];
Y(t)=y(t);
end
teta=(Phi.’*Phi)\Phi.’*Y;
teta4=teta;
disp(‘Q1: Least squares estimation for N=400’);
disp(‘estimated a=’);disp(teta(1));
disp(‘estimated b=’);disp(teta(2));
ترسیم درصد خطای نسبی تخمین پارامترها بر حسب تعداد داده ها
Nv=[100,200,300,400];
Er_Nv_a=[abs(a-teta1(1))/a,abs(a-teta2(1))/a,abs(a-teta3(1))/a,abs(a-teta4(1))/a]*100;
Er_Nv_b=[abs(b-teta1(2))/b,abs(b-teta2(2))/b,abs(b-teta3(2))/b,abs(b-teta4(2))/b]*100;
figure (2)
subplot(2,1,1);bar(Nv,Er_Nv_a,’b’);xlabel(‘N’);ylabel(‘a relative error (%)’);
subplot(2,1,2);bar(Nv,Er_Nv_b,’b’);xlabel(‘N’);ylabel(‘b relative error (%)’);
%Recursive least squaresروش حداقل مربعات بازگشتی
lmbd=0.98;ضریب فراموشی
P=1e6*eye(2); ماتریس
teta_rls1=zeros(2,N1);ماتریس تخمین ها
تخمین حداقل مربعات بازگشتی
for t=2:N1
phi=[-y1(t-1);u1(t-1)];
Kt=P*phi/(lmbd*eye(1)+phi.’*P*phi);
P=(eye(2)-Kt*phi.’)*P/lmbd;
teta_rls1(:,t)=teta_rls1(:,t-1)+Kt*(y1(t)-phi.’*teta_rls1(:,t-1));
end
ترسیم پارامترهای تخمینی به روش حداقل مربعات و مقادیر واقعی و مقادیر روش قبل
figure (3)
subplot(2,1,1);stairs(1:N1,teta1(1)*ones(1,N1),’b’,’linewidth’,2);grid on;
hold on;
stairs(1:N1,teta_rls1(1,:),’g’,’linewidth’,2);
hold on;
stairs(1:N1,a*ones(1,N1),’r’,’linewidth’,2);
legend(‘LS for N=100′,’RLS for N=100′,’a=0.7’);
subplot(2,1,2);stairs(1:N1,teta1(2)*ones(1,N1),’b’,’linewidth’,2);grid on;
hold on;
stairs(1:N1,teta_rls1(2,:),’g’,’linewidth’,2);
hold on;
stairs(1:N1,b*ones(1,N1),’r’,’linewidth’,2);
legend(‘LS for N=100′,’RLS for N=100′,’b=2’);
%==========================================================================
%Q2سوال شماره 2
u=[1,0.8,0.6,0.4,0.2,0,0.2,0.4,0.6,0.8,1,0.8,0.6,0.4,0.2];
y=[0.9,2.5,2.4,1.3,1.2,0.8,0,0.9,1.4,1.9,2.3,2.4,2.3,1.3,1.2];
N=length(u);
ترسیم داده های شناسایی
figure (4)
subplot(2,1,1);stairs(1:1:N,y,’b’,’linewidth’,2);grid on;axis([1 N -1 4]);ylabel(‘y’);
subplot(2,1,2);stairs(1:1:N,u,’b’,’linewidth’,2);grid on;axis([1 N -1 2]);ylabel(‘u’);xlabel(‘sample’);
Phi=zeros(N-1,3);
Y=zeros(N-1,1);
for t=2:N
Phi(t,:)=[-y(t-1),u(t),u(t-1)];
Y(t)=y(t);
end
teta=(Phi.’*Phi)\Phi.’*Y;تخمین پارامترها
disp(‘Q2: Least squares estimation’);
disp(‘estimated a1=’);disp(teta(1));
disp(‘estimated b0=’);disp(teta(2));
disp(‘estimated b1=’);disp(teta(3));
%==========================================================================
%Q3سوال شماره 3
پارامترها
a=-0.9;
b0=1;
b1=0.5;
c=1;
sigm_e=1;
N=200;
y=zeros(1,N);
u=idinput(N);
ep=wgn(1,N,0);
sigm_ep=1/(N)*sum(ep.^2);
e=sqrt(sigm_e/(sigm_ep))*ep;
for t=3:N
y(t)=-a*y(t-1)+b0*u(t-1)+b1*u(t-2)+c*e(t);
end
figure (5)
subplot(2,1,1);stairs(1:1:N,y,’b’,’linewidth’,2);grid on;axis([1 N -20 20]);ylabel(‘y’);
subplot(2,1,2);stairs(1:1:N,u,’b’,’linewidth’,2);grid on;axis([1 N -2 2]);ylabel(‘u’);xlabel(‘sample’);
% Model A — Least squares تخمین جداقل مربعات برای مدل اول
Phi=zeros(N-1,3);
Y=zeros(N-1,1);
for t=3:N
Phi(t,:)=[-y(t-1),u(t-1),u(t-2)];
Y(t)=y(t);
end
teta=(Phi.’*Phi)\Phi.’*Y;
disp(‘Q3: Least squares estimation’);
disp(‘estimated a=’);disp(teta(1));
disp(‘estimated b0=’);disp(teta(2));
disp(‘estimated b1=’);disp(teta(3));
%Model A — Extended Least squares تخمین حداقل مربعات تعمیم یافته برای مدل اول
Phi=zeros(N-1,4);
Y=zeros(N-1,1);
teta0=[teta(1);teta(2);teta(3);1];
teta=teta0;
for t=3:N
Phi(t,:)=[-y(t-1),u(t-1),u(t-2),y(t-1)-Phi(t-1,:)*teta];
Y(t)=y(t);
if (t<10)
teta=teta0;
else
teta=(Phi(1:t,:).’*Phi(1:t,:))\Phi(1:t,:).’*Y(1:t);
end
end
disp(‘Q3: Extended Least squares estimation’);
disp(‘estimated a=’);disp(teta(1));
disp(‘estimated b0=’);disp(teta(2));
disp(‘estimated b1=’);disp(teta(3));
disp(‘estimated c=’);disp(teta(4));
%Model A — Instrumental variables روش متغیرهای کمکی
Phi=zeros(N-1,3);
Z=zeros(N-1,3);
Y=zeros(N-1,1);
for t=4:N
Phi(t,:)=[-y(t-1),u(t-1),u(t-2)];
Z(t,:)=[u(t-1),u(t-2),u(t-3)]; متغیرهای کمکی انتخاب شده
Y(t)=y(t);
end
teta=(Z.’*Phi)\Z.’*Y;تخمین پارامترها
disp(‘Q3: Instrumental variable estimation’);
disp(‘estimated a=’);disp(teta(1));
disp(‘estimated b0=’);disp(teta(2));
disp(‘estimated b1=’);disp(teta(3));
% Model B — Least squares روش حداقل مربعات برای مدل دوم
Phi=zeros(N-1,3);
Y=zeros(N-1,1);
for t=3:N
Phi(t,:)=[-y(t-1),u(t-1),u(t-2)];
Y(t)=y(t);
end
teta=(Phi.’*Phi)\Phi.’*Y;
disp(‘Q3: Least squares estimation’);
disp(‘estimated a=’);disp(teta(1));
disp(‘estimated b0=’);disp(teta(2));
disp(‘estimated b1=’);disp(teta(3));
%Model B — Extended Least squares روش حداقل مربعات تعمیم یافته برای مدل دوم
Phi=zeros(N-1,5);
Y=zeros(N-1,1);
teta0=[teta(1);teta(2);teta(3);1;1];
teta=teta0;
for t=3:N
Phi(t,:)=[-y(t-1),u(t-1),u(t-2),y(t-1)-Phi(t-1,:)*teta,y(t-2)-Phi(t-2,:)*teta];
Y(t)=y(t);
if (t<10)
teta=teta0;
else
teta=(Phi(1:t,:).’*Phi(1:t,:))\Phi(1:t,:).’*Y(1:t);
end
end
disp(‘Q3: Extended Least squares estimation’);
disp(‘estimated a=’);disp(teta(1));
disp(‘estimated b0=’);disp(teta(2));
disp(‘estimated b1=’);disp(teta(3));
disp(‘estimated c0=’);disp(teta(4));
disp(‘estimated c1=’);disp(teta(5));
%Model B — Instrumental variables روش متغیرهای کمکی برای مدل دوم
Phi=zeros(N-1,5);
Z=zeros(N-1,5);
Y=zeros(N-1,1);
teta0=[teta(1);teta(2);teta(3);1;1];
teta=teta0;
for t=6:N
Phi(t,:)=[-y(t-1),u(t-1),u(t-2),y(t-1)-Phi(t-1,:)*teta,y(t-2)-Phi(t-2,:)*teta];
Z(t,:)=[u(t-1),u(t-2),u(t-3),y(t-4),y(t-5)]; متغیرهای کمکی
Y(t)=y(t);
if (t<10)
teta=teta0;
else
teta=(Z(1:t,:).’*Phi(1:t,:))\Z(1:t,:).’*Y(1:t);
end
end
disp(‘Q3: Instrumental variables estimation’);
disp(‘estimated a=’);disp(teta(1));
disp(‘estimated b0=’);disp(teta(2));
disp(‘estimated b1=’);disp(teta(3));
disp(‘estimated c0=’);disp(teta(4));
disp(‘estimated c1=’);disp(teta(5));
نگران نباشید ما این کد آماده متلب را در انتهای همین پست برای شما قرار داده ایم.
نتایج شبیه سازی را در زیر قرار داده ایم:
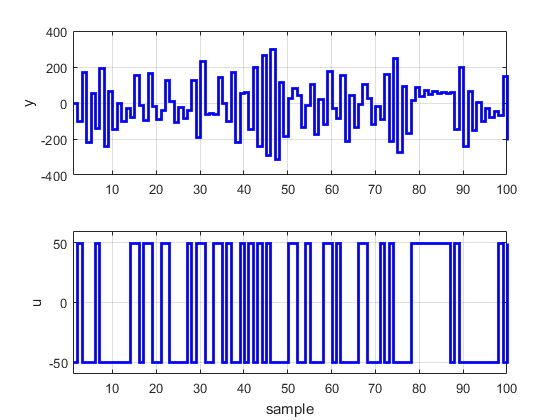

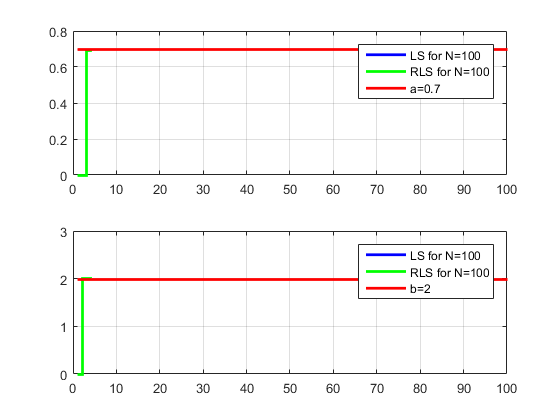
شاید علاقه مند باشید مطالب دیگر سایت متلبی را نیز ببینید:
- پروژه کامپیوتری درس فرایند تصادفی با متلب
- طراحی و شبیه سازی درایو موتور رلوکتانس سوییچی با متلب
- شبیه سازی رفتار یک رله مغناطیسی با متلب
- سفارش شبیه سازی مقالات درس کنترل توان راکتیو
- تشخیص فونم ها(لب خوانی) با SVM در متلب
- شناسایی سیستم غیر خطی ربات بازوی مسطح دو درجه آزادی توسط شبکه عصبی
- شبیه سازی سیستم درایو کرامر استاتیکی با متلب
- حل تابع با سری تیلور و روش نیوتن در متلب
- توابع نمایی در متلب
- مشکل لایسنس متلب در زمان اجرای نرم افزار متلب
- پیش بینی سری زمانی به کمک شبکه عصبی در متلب

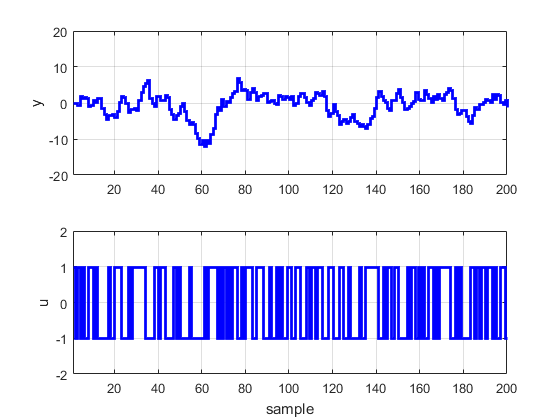
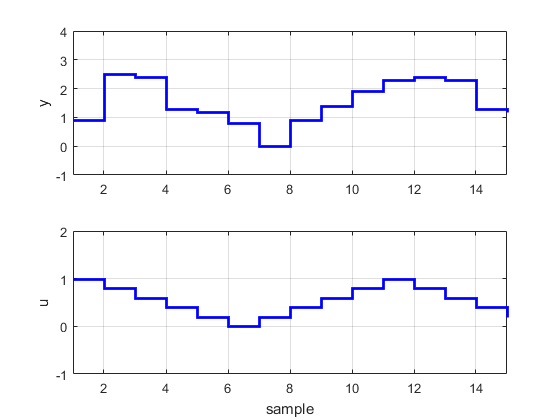


بی نهایت سپاس
نظر لطف شماست