توضیحات
عملکرد کنترل کننده PID مرتبه کسری بهینه در مدل مرتبه کسری بیماری HIV با الگوریتم GA و PSO
شبیه سازی در محیط سیمولینک متلب انجام شده است. متلب2018
دارای گزارش 11 صفحه ای در قالب ورد است.
توضیح پروژه تنظیم ضرایب کنترل کننده PID مرتبه کسری بهینه در مدل مرتبه کسری بیماری HIV
مقدمه:
کنترل بیماری HIV همواره یک مساله ی مهم در مبحث سیستمهای کنترل و پزشکی بوده است.
با توجه به این علم استفاده از حسابان کسری به صورت خیلی وسیعی در حال استفاده و گسترش می باشد و از طرفی در مراجع مختلف به صراحت بیان شده که سیستم ها در عالم واقع به صورت مرتبه کسری هستند به همین منظور در این مقاله برای این که نتایج شبیه سازی واقعی تر
باشند از مدل مرتبه کسری بیماری HIVاستفاده شده است.
معادلات بیان شده برای مدل بیماری HIV به گونه ای است که رفتار سیستم به شدت به تعداد ویروس های تولید شده توسط سلول های الوده وابسته است به صورتی که اگر تعداد ویروس ها از 202 ویروس بیشتر باشد رفتار بیماری به گونه ای است که باعث انتشار ویروس و بیماری می شود.
برای کنترل بیماری HIV از کنترل کننده PD مرتبه کسری بهینه استفاده شده است که ضرایب این کنترل کننده توسط الگوریتم بهینه سازی ژنتیک و الگوریتم ازدحام ذرات بدست امده است.
توضیحات مربوط به شبیه سازی با متلب
شبیه سازی مربوط به این مقاله در پوشه ای بنام simulation است، که شامل دو ام-فایل متلب و دو مدل سیمولینک متلب وجود دارد که به توضیح آن ها خواهیم پرداخت.
مدل سیمولینک hiv_model_no_control_2018b
از آن جا که مدل مربوط به مقاله مرتبه کسری است و نه صحیح، در نتیجه باید از بلوک مشتق گیر مرتبه کسری استفاده شود. نحوه نصب جعبه ابزار مربوط به این بلوک (fomcon toolbox) در یک ویدیو همراه فایل های این پروژه آورده شده است. بخش اصلی مدل های سیمولینک به صورت کدنویسی متلب (در بلوک matlab function) است ولی در کنار آن از بلوک مشتق گیر مرتبه کسری هم استفاده شده است.
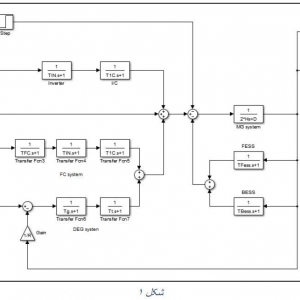
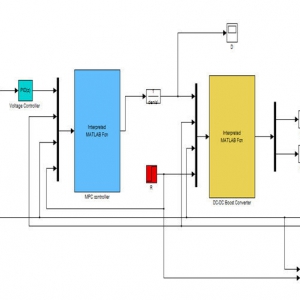
در گزارش ورد همراه پروژه, بخش های سیمولینک و کد متلب به صورت عکس آورده شده و در مورد آن توضیح داده شده است. برای نمونه بخشی از تصویر مربوط به سیمولینک آورده شده و در زیر آن توضیح به صورت زیر قرار داده شده است:
قسمت 1: همان كدنويسي متلب مي باشد كه ثابت های جدول (1) و معادله (2) مقاله در آن نوشته شده است.
توضیحات کامل در گزارش اصلی پروژه آمده است.
مدل سیمولینک hiv_model_pid_control_2018b
تمام موارد مانند قبل است. فقط در این مدل، بلوک کنترلر PID قرار داده شده است.
توضیحات فایل hiv_cost_function
این فایل تابع هزینه جهت بهینه سازی می باشد که برای هر 2 روش GA و PSO به کار گرفته می شود. ورودی این تابع K و خروجی آن f (مقدار تابع هزینه) است.
خطوط 6 تا 8: ورودی تابع سه عضو دارد که همان ضرایب PID می باشند. در این خطوط هر عضو K نام گذاری می گردد.
خط 11: حل مدل سیمولینک کنترلی با مقادیر بهینه ضرایب کنترلر در لحظه کنونی.
خط 14: طبق گفته مقاله، تابع هزینه 3 بخش دارد که یک بخش مربوط به متغیر x است که باید ماکزیمم گردد و دو بخش دیگر مربوط به y و z می باشند که باید مینیمم گردند. این خط مربوط به تابع هزینه x است و هدف آن ماکزیمم نمودن مقدار نهایی x به توان 2 است (برای ماکزیمم شدن علامت منفی قرار داده می شود).
خطوط 15 و 16: مقادیر تابع هزینه برای y و z که به صورت مینیمم شدن توان 2 مقدار نهایی آن ها با علامت در نظر گرفته شده اند.
خط 17: جمع مقادیر تابع هزینه سه متغیر حالت و محاسبه تابع هزینه نهایی.
توضیحات فایل main
برای اجرای شبیه سازی فقط این فایل باید اجرا شود (نه مدل های سیمولینک و یا فایل تابع هزینه)
خط 10: مقدار N که طبق مقاله، برای مقادیر زیر 202 نیازی به استفاده از کنترلر نیست و برای مقادیر بالای 202 سیستم ناپایدار شده و کنترلر مورد استفاده قرار می گیرد.
خط 16: متغیر تعریف شده در این خط باید یکی از مقادیر 1 تا 3 را داشته باشد:
مقدار 1: حل مساله بدون کنترل
مقدار 2: حل مساله کنترلی با بهینه سازی الگوریتم ژنتیک
مقدار 3: حل مساله کنترلی با بهینه سازی ازدحام ذرات
خطوط 19 تا 40: حل مساله بهینه سازی و اجرای مدل سیمولینک طبق انتخاب قبلی شما. در خط 25 روش الگوريتم ژنتيك و در خط 33 روش ازدحام ذرات اجرا مي گردند. يك قيد به صورت [0.001,0.001,0.001] در اين خطوط قرار داده شده است كه به معني مقدار مينيمم ضرايب PID مي باشد (يعني ضرايب حتما مثبت باشند). روش حد بالاي ضرايب قيدي تعريف نشده است.
خطوط 43 تا انتها: چاپ و رسم نتایج.
نتایج شبیه سازی با متلب
شما می توانید با انتخاب مقدار N و نیز نوع مساله (1 تا 3)، هر کدام از نمودارها را مشاهده نمایید. برای مثال:
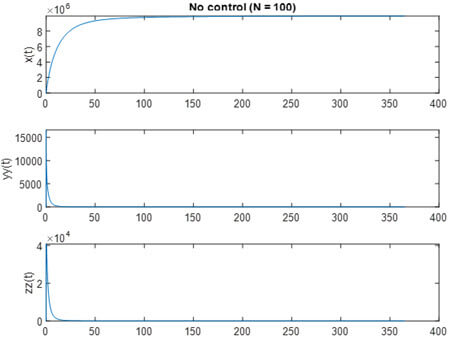
حالت بدون کنترلی با N = 100
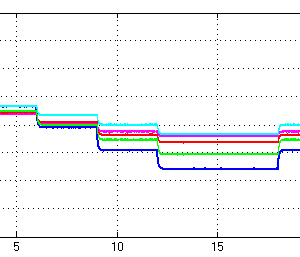
ملاحظه می شود بسیار شبیه به نتیجه مقاله شده است. هم چنین نتایج زیر هم مانند مقاله هستند:
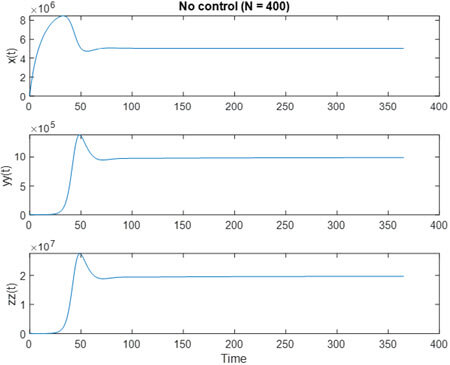
حالت بدون کنترلی با N = 400
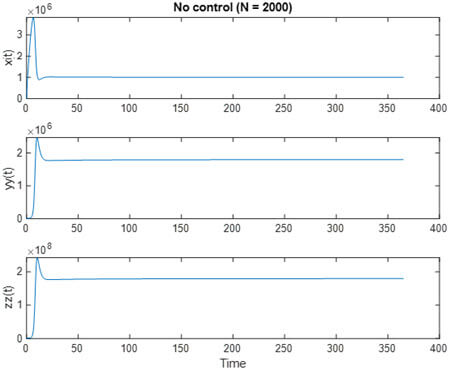
حالت بدون کنترلی با N = 2000
نتايج كنترلي: براي مثال نتايج مربوط به هر روش بهينه سازي با N = 2000 نشان داده مي شود. ساير نتايج را مي توانيد به راحتي توليد نماييد. دقت كنيد كه به دليل ماهيت يك مساله بهينه سازي ممكن است در هر اجرا ضرايب كنترلر قدري متفاوت شوند و در نتيجه نتايج دقيق مثل هم نباشند ولي نكته مهم در اين است كه كليت تمام نتايج يكسان هستند. هم چنين زمان شبيه سازي هاي بهينه قدري زياد است كه بايد صبر نماييد.
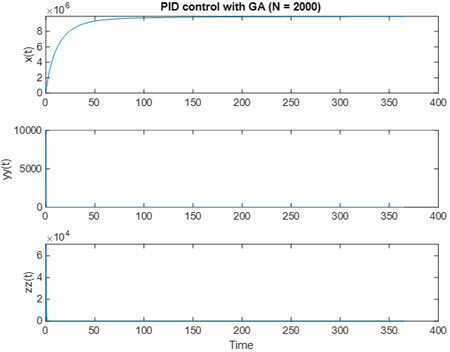
مساله كنترلي GA با N = 2000

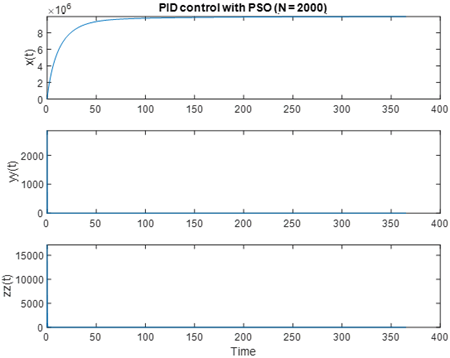
مساله كنترلي PSO با N = 2000
شاید به موارد زیر نیز علاقه مند باشید:
- طراحی ناظر تابعی با مرتبه کسری ورودی نامشخص برای سیستم های مرتبه کسری با تاخیر زمانی لیپشیتس یک طرفه
- یک توپولوژی مبتنی بر کنترل مود لغزشی مرتبه کسری برای بهبود پایداری گذرا سیستمهای انرژی باد
- مقایسه عملکرد توربین بادی مبتنی بر ژنراتور القایی از دو سو تغذیه با استفاده از کنترل کننده های تحمل خطای مرتبه کسری و صحیح
- کنترل مود لغزشی مرتبه کسری برای کنترل وضعیت ماهوارهای اسمی و کم کار
- طراحی PID کنترلر برای ستون تقطیر با GA
- بدست آوردن تقریب سری تیلور مرتبه دوم با متلب
کلیدواژه:
مدل مرتبه کسری,بیماری HIV ,کنترل کننده مرتبه کسری
عملکرد کنترل کننده PID مرتبه کسری بهینه در مدل مرتبه کسری بیماری HIV با الگوریتم GA و PSO با متلب
طبق توضیحات فوق توسط کارشناسان سایت متلبی تهیه شده است و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،.
با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.


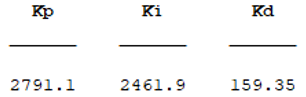



نقد و بررسیها
هنوز بررسیای ثبت نشده است.